题目内容
(本题满分12分)w.w.^w.k.&s.5*u.c.#om高.考.资.源.网
已知函数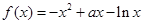 (
(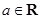 ).
).
(1)当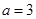 时,求函数
时,求函数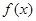 在
在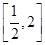 上的最大值和最小值;
上的最大值和最小值;
(2)当函数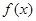 在
在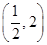 单调时,求
单调时,求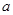 的取值范围;
的取值范围;
(3)求函数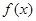 既有极大值又有极小值的充要条件。
既有极大值又有极小值的充要条件。
(1)函数在 最大值是
最大值是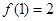 ,函数在
,函数在 上的最小值为
上的最小值为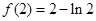 。w.w.^w.k.&s.5*u.c.#om高.考.资.源.网
。w.w.^w.k.&s.5*u.c.#om高.考.资.源.网
(2) 的取值范围是
的取值范围是 。
。
(3)函数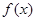 既有极大值又有极小值的充要条件
既有极大值又有极小值的充要条件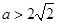 。
。
【解析】(1) 时,
时, ,
,
函数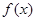 在区间
在区间 仅有极大值点
仅有极大值点 ,故这个极大值点也是最大值点,
,故这个极大值点也是最大值点,
故函数在 最大值是
最大值是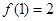 ,w.w.^w.k.&s.5*u.c.#om高.考.资.源.网
,w.w.^w.k.&s.5*u.c.#om高.考.资.源.网
又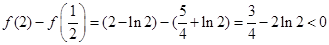 ,故
,故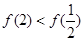 ,
,
故函数在 上的最小值为
上的最小值为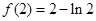 。
……………4分
。
……………4分
(2) ,令
,令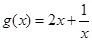 ,则
,则 ,
,
则函数在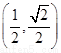 递减,在
递减,在 递增,由
递增,由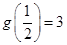 ,
, ,
,
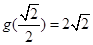 ,故函数
,故函数 在
在 的值域为
的值域为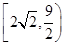 。
。
若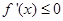 在
在 恒成立,即
恒成立,即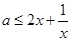 在
在 恒成立,
恒成立,
只要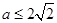 ,若要
,若要 在在
在在 恒成立,即
恒成立,即 在
在 恒成立,
恒成立,
只要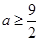 。即
。即 的取值范围是
的取值范围是 。 ……………8分
。 ……………8分
(3)若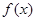 既有极大值又有极小值,则首先必须
既有极大值又有极小值,则首先必须 有两个不同正根
有两个不同正根 ,
,
即  有两个不同正根。w.w.^w.k.&s.5*u.c.#om高.考.资.源.网
有两个不同正根。w.w.^w.k.&s.5*u.c.#om高.考.资.源.网
故 应满足
应满足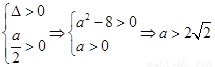 ,
,
∴当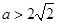 时,
时, 有两个不等的正根,不妨设
有两个不等的正根,不妨设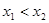 ,
,
由
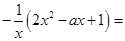

 知:
知: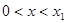 时
时 ,
,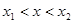 时
时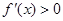 ,
,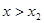 时
时 ,
,
∴当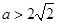 时
时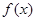 既有极大值
既有极大值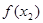 又有极小值
又有极小值 .
.
反之,当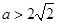 时,
时, 有两个不相等的正根,
有两个不相等的正根,
故函数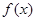 既有极大值又有极小值的充要条件
既有极大值又有极小值的充要条件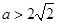 。
……………12分
。
……………12分

(本题满分12分)
为迎接国庆60周年,美化城市,某市将一矩形花坛ABCD扩建成一个更大的矩形花园AMPN,如图所示。要求B在AM上,D在AN上,且对角线MN过C点,|AB|=3米,|AD|=2米.
(Ⅰ)要使矩形AMPN的面积大于32平方米,则AN的长应在什么范围内?w.w.w.k.s.5.u.c.o.m ![]()
|
(Ⅱ)若AN的长度不小于6米,则当AM、AN的长度是多少时,矩形AMPN的面积最小?并求出最小面积.

 }(
}( 是正整数)是首项是
是正整数)是首项是 ,公比是
,公比是 的等比数列
的等比数列 w_w w. k#s5_u.c o
w_w w. k#s5_u.c o ;
; ;
;