题目内容
10.△ABC中,角A、B、C的对边a、b、c,且3acosA=$\sqrt{6}$(bcosC+ccosB).(1)求cosA的值;
(2)若$sin(\frac{π}{2}+B)=\frac{1}{3}$,c=2$\sqrt{2}$,求△ABC的面积.
分析 (1)根据正弦定理进行求解即可求cosA的值;
(2)根据两角和差的正弦公式以及正弦定理,三角形的面积公式进行求解即可.
解答 解:(1)由正弦定理得$3sinAcosA=\sqrt{6}sin(B+C)$,
得$cosA=\frac{{\sqrt{6}}}{3}$.
(2)若$sin(\frac{π}{2}+B)=\frac{1}{3}$,
则$cosB=\frac{1}{3},sinB=\frac{{2\sqrt{2}}}{3}$,
${sinC}=sin(A+B)=sinAcosB+cosAsinB=\frac{{5\sqrt{3}}}{9}$
又$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}$得$a=\frac{{6\sqrt{2}}}{5},b=\frac{{8\sqrt{3}}}{5}$,
${S_△}=\frac{1}{2}absinC=\frac{8}{5}\sqrt{2}$.
点评 本题主要考查解三角形的应用,根据正弦定理以及三角形的面积公式是解决本题的关键.

练习册系列答案
相关题目
4.复数z=2-i(i是虚数单位)在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
1.因为对数函数y=logax(a>0,且a≠1)是增函数,而y=log${\;}_{\frac{1}{2}}$x是对数函数,所以y=log${\;}_{\frac{1}{2}}$x是增函数,上面的推理错误的是( )
| A. | 大前提 | B. | 小前提 | C. | 推理形式 | D. | 以上都是 |
5.如图给出的是计算和式$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{20}$的值的一个程序框图,其中判断框内应填入的条件是( )
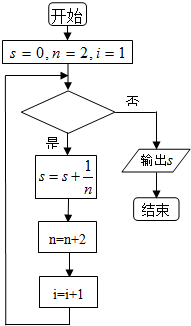

| A. | i≤11 | B. | i≤10 | C. | i≥10 | D. | i≥11 |
15.某人练习射击,共有5发子弹,每次击中目标的概率为0.6,若他只需要在五次射击中四次击中目标就算合格,一旦合格即停止练习.则他在第五次射击结束时恰好合格的概率为( )
| A. | 0.64×0.4 | B. | C${\;}_{5}^{4}$•0.64•(1-0.6)+C${\;}_{5}^{5}$•0.65 | ||
| C. | 0.64 | D. | C${\;}_{4}^{3}$×0.64×0.4 |
20.已知x1,x2分别是函数f(x)=$\frac{1}{3}$x3+$\frac{1}{2}$ax2+2bx+c的两个极值点,且x1∈(0,1)x2∈(1,2),则$\frac{b-2}{a-1}$的取值范围为( )
| A. | (1,4) | B. | ($\frac{1}{2}$,1) | C. | ($\frac{1}{4}$,$\frac{1}{2}$) | D. | ($\frac{1}{4}$,1) |
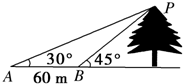 如图所示,为测一树的高度,在地面上选取A、B两点,从A、B两点分别测得树尖的仰角为30°,45°,且A、B两点之间的距离为60m,求树的高度.
如图所示,为测一树的高度,在地面上选取A、B两点,从A、B两点分别测得树尖的仰角为30°,45°,且A、B两点之间的距离为60m,求树的高度.