题目内容
如图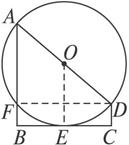
图
A.![]() B
B![]()
解析:连结DF、OE,
∵AD是直径,∴∠AFD=90°.
又AB⊥BC,DC⊥BC,∴四边形BCDF是矩形.
∴BF=DC.由切割线定理得
BE2=BF·BA=1×4=4,BE=2.
∵OE⊥BC,DC⊥BC,AB⊥BC,
∴CD∥OE∥AB.O为AD中点,
∴E为BC中点.
∴BC=4.∴DF=4.
在Rt△ADF中,AD=![]() =5.
=5.
答案:C

练习册系列答案
相关题目
题目内容
如图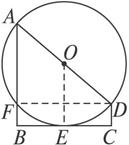
图
A.![]() B
B![]()
解析:连结DF、OE,
∵AD是直径,∴∠AFD=90°.
又AB⊥BC,DC⊥BC,∴四边形BCDF是矩形.
∴BF=DC.由切割线定理得
BE2=BF·BA=1×4=4,BE=2.
∵OE⊥BC,DC⊥BC,AB⊥BC,
∴CD∥OE∥AB.O为AD中点,
∴E为BC中点.
∴BC=4.∴DF=4.
在Rt△ADF中,AD=![]() =5.
=5.
答案:C
