题目内容
已知函数g(x)=
,若g(a)≥g(
),则实数a的取值范围是
|
| 1 |
| a |
[-
,0)∪[1,+∞)
| 2 |
[-
,0)∪[1,+∞)
.| 2 |
分析:根据分段函数g(x)的解析式作出其图象,如图所示.再对x进行分类讨论:①当x>-
时,g(x)是增函数,若g(a)≥g(
);②当x≤-
时,g(x)=
,若g(a)≥g(
),得出关于a的不等关系,最后综上①②所述,即可得出实数a的取值范围.
| ||
| 2 |
| 1 |
| a |
| ||
| 2 |
| 2 |
| 1 |
| a |
解答: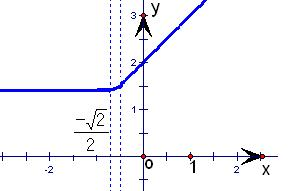 解:根据函数g(x)的解析式作出其图象,如图所示.
解:根据函数g(x)的解析式作出其图象,如图所示.
①当x>-
时,g(x)是增函数,
若g(a)≥g(
),
则
,解得:-1≤a<0或a≤≥1;
②当x≤-
时,g(x)=
,
若g(a)≥g(
),
则
,解得:-
≤a≤-
;
综上①②所述,实数a的取值范围是[-
,0)∪[1,+∞)
故答案为:[-
,0)∪[1,+∞).
 解:根据函数g(x)的解析式作出其图象,如图所示.
解:根据函数g(x)的解析式作出其图象,如图所示.①当x>-
| ||
| 2 |
若g(a)≥g(
| 1 |
| a |
则
|
②当x≤-
| ||
| 2 |
| 2 |
若g(a)≥g(
| 1 |
| a |
则
|
| 2 |
| ||
| 2 |
综上①②所述,实数a的取值范围是[-
| 2 |
故答案为:[-
| 2 |
点评:本小题主要考查函数单调性的应用、不等式的解法等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目