题目内容
如图A、B、C是固定在桌面上的三根立柱,其中A柱上有三个大小不同的圆片,下面的直径总比上面的大,现将三个圆片移动到B柱上,要求每次只移动一片(叫移动一次),被移动的圆片只能放入A、B、C三个柱子之一,且大圆片不能叠在小圆片的上面,那么完成这件事情至少要移动的次数是( )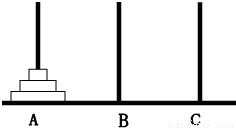
A..3
B..5
C.、7
D..9
【答案】分析:应先把最小的移动到B,较大的移动到C,然后把最小的移动到C上,把最大的移动到B,把较小的移动到A,把较大的移动到B,最后把最小的移动到B共需7次.
解答:解:需分两步完成:(设最大的圆片为3,较小的为2,最小的为1)
①先将最小的圆片移动到B柱上:1⇒B,2⇒C,1⇒C,3⇒B,此时完成了第一步,移动了4次;
②将最大圆片放到B柱后,再将剩下两个,按序排列:1⇒A,2⇒B,1⇒B;此时完成了第二步,移动了3次,
因此一共移动了3+4=7次.
故选C.
点评:本题考查了进行简单的合情推理,解答的关键是利用直接法进行模拟操作即可.属于基础题.
解答:解:需分两步完成:(设最大的圆片为3,较小的为2,最小的为1)
①先将最小的圆片移动到B柱上:1⇒B,2⇒C,1⇒C,3⇒B,此时完成了第一步,移动了4次;
②将最大圆片放到B柱后,再将剩下两个,按序排列:1⇒A,2⇒B,1⇒B;此时完成了第二步,移动了3次,
因此一共移动了3+4=7次.
故选C.
点评:本题考查了进行简单的合情推理,解答的关键是利用直接法进行模拟操作即可.属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
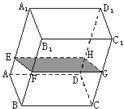 10、如图,在透明塑料制成的长方体ABCD-A1B1C1D1容器内灌进一些水,将容器底面一边BC固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法:
10、如图,在透明塑料制成的长方体ABCD-A1B1C1D1容器内灌进一些水,将容器底面一边BC固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法:
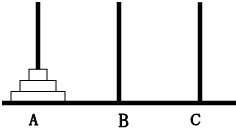 如图A、B、C是固定在桌面上的三根立柱,其中A柱上有三个大小不同的圆片,下面的直径总比上面的大,现将三个圆片移动到B柱上,要求每次只移动一片(叫移动一次),被移动的圆片只能放入A、B、C三个柱子之一,且大圆片不能叠在小圆片的上面,那么完成这件事情至少要移动的次数是( )
如图A、B、C是固定在桌面上的三根立柱,其中A柱上有三个大小不同的圆片,下面的直径总比上面的大,现将三个圆片移动到B柱上,要求每次只移动一片(叫移动一次),被移动的圆片只能放入A、B、C三个柱子之一,且大圆片不能叠在小圆片的上面,那么完成这件事情至少要移动的次数是( )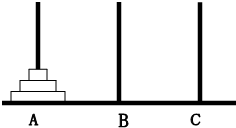 如图A、B、C是固定在桌面上的三根立柱,其中A柱上有三个大小不同的圆片,下面的直径总比上面的大,现将三个圆片移动到B柱上,要求每次只移动一片(叫移动一次),被移动的圆片只能放入A、B、C三个柱子之一,且大圆片不能叠在小圆片的上面,那么完成这件事情至少要移动的次数是
如图A、B、C是固定在桌面上的三根立柱,其中A柱上有三个大小不同的圆片,下面的直径总比上面的大,现将三个圆片移动到B柱上,要求每次只移动一片(叫移动一次),被移动的圆片只能放入A、B、C三个柱子之一,且大圆片不能叠在小圆片的上面,那么完成这件事情至少要移动的次数是