题目内容
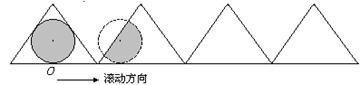
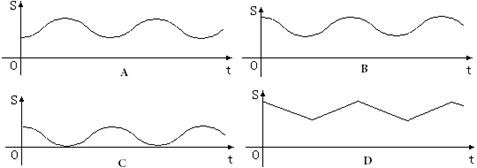
一电子广告,背景是由固定的一系列下顶点相接的正三角形组成,这列正三解形的底边在同一直线上,正三角形的内切圆由第一个正三角形的O点沿三角形列的底边匀速向前滚动(如图),设滚动中的圆与系列正三角形的重叠部分(如图中的阴影)的面积S关于时间t的函数为S=f(t),则下列图中与函数S=f(t)图象最近似的是( )


分析:根据滚动中的圆与系列正三角形的重叠部分(如图中的阴影)的面积S关于时间t的关系为非线性关系,可排除D答案;根据函数的最小值不为0,可排除C,根据t=0时,函数取最大值,可排除A.
解答:解:滚动中的圆与系列正三角形的重叠部分(如图中的阴影)的面积S关于时间t的关系呈周期性变化,
且两者之间是非线性变化,故排除答案D;
当圆滚动到两三角形的连接点时,阴影部分的面积取最小值,但仍不为0,故排除答案C
又由当t=0时,阴影部分的面积取最大值,可排除答案A
故选:B
且两者之间是非线性变化,故排除答案D;
当圆滚动到两三角形的连接点时,阴影部分的面积取最小值,但仍不为0,故排除答案C
又由当t=0时,阴影部分的面积取最大值,可排除答案A
故选:B
点评:本题考查的知识点是函数的图象,其中根据题意分析出函数的周期性,最值…并也图象一一比照,利用排除法求解是解答的关键.

练习册系列答案
相关题目
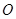 点沿三角形列的底边匀速向前滚动(如图),设滚动中的圆与系列正三角形的重叠部分(如图中的阴影)的面积
点沿三角形列的底边匀速向前滚动(如图),设滚动中的圆与系列正三角形的重叠部分(如图中的阴影)的面积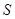 关于时间
关于时间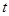 的函数为
的函数为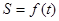 ,则下列图中与函数
,则下列图中与函数