题目内容
已知函数 (
( ),该函数所表示的曲线上的一个最高点为
),该函数所表示的曲线上的一个最高点为 ,由此最高点到相邻的最低点间曲线与x轴交于点(6,0)。
,由此最高点到相邻的最低点间曲线与x轴交于点(6,0)。
(1)求 函数解析式;
函数解析式;
(2)求函数 的单调区间;
的单调区间;
(3)若 ,求
,求 的值域。
的值域。
(1) 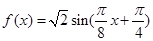 ;(2)单调递增区间:
;(2)单调递增区间: , 单调递减区间:
, 单调递减区间: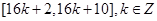 ;(3)
;(3)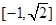
解析试题分析:(1)由曲线y=Asin(ωx+φ)的一个最高点是 ,得A=
,得A=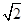 ,又最高点
,又最高点 到相邻的最低点间,曲线与x轴交于点(6,0),则
到相邻的最低点间,曲线与x轴交于点(6,0),则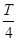 =6-2=4,即T=16,所以ω=
=6-2=4,即T=16,所以ω=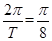 .此时y=
.此时y=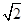 sin(
sin(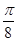 x+φ),将x=2,y=
x+φ),将x=2,y=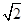 代入得
代入得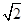 =
=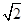 sin(
sin(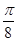 ×2+φ),
×2+φ), ,
,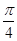 +φ=
+φ= ,∴φ=
,∴φ=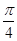 ,所以这条曲线的解析式为
,所以这条曲线的解析式为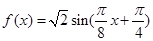 .
.
(2)因为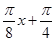 ∈[2kπ-
∈[2kπ- ,2kπ+
,2kπ+ ],解得x∈[16k-6,2+16k],k∈Z.所以函数的单调增区间为[-6+16k,2+16k],k∈Z,因为
],解得x∈[16k-6,2+16k],k∈Z.所以函数的单调增区间为[-6+16k,2+16k],k∈Z,因为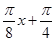 ∈[2kπ+
∈[2kπ+ ,2kπ+
,2kπ+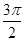 ],解得x∈[2+16k,10+16k],k∈Z,
],解得x∈[2+16k,10+16k],k∈Z,
所以函数的单调减区间为:[2+16k,10+16k],k∈Z,
(3)因为 ,由(2)知函数f(x)在[0.2]上单调递增,在[2,8]上单调递减,所以当x=2时,f(x)有最大值为
,由(2)知函数f(x)在[0.2]上单调递增,在[2,8]上单调递减,所以当x=2时,f(x)有最大值为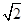 ,当x=8时,f(x)有最小值为-1,故f(x)的值域为
,当x=8时,f(x)有最小值为-1,故f(x)的值域为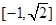
考点:本题考查了求函数y=Asin(ωx+φ)的解析式的方法.函数单调区间的求法
点评:求解三角函数的单调性、奇偶性、周期性、对称性问题,一般都要经过三角恒等变换,转化为y=Asin(ωx+Φ)型等,然后根据基本函数y=sinx等相关的性质进行求解

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的扇形,C是扇形弧上的动点,ABCD是扇形的内接矩形,记
的扇形,C是扇形弧上的动点,ABCD是扇形的内接矩形,记 ,求当角
,求当角 取何值时, 矩形ABCD的面积最大?并求出这个最大值.
取何值时, 矩形ABCD的面积最大?并求出这个最大值.
 为第三象限角,
为第三象限角, .
. ;
;  ,求
,求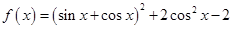 .
. 的最小正周期;
的最小正周期;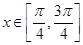 时,求函数
时,求函数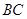 与灯柱
与灯柱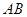 所在平面与道路垂直,且
所在平面与道路垂直,且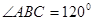 ,路灯
,路灯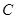 采用锥形灯罩,射出的光线如图阴影部分所示,已知
采用锥形灯罩,射出的光线如图阴影部分所示,已知 ,路宽
,路宽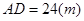 ,设灯柱高
,设灯柱高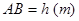 ,
, .
.
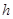 (用
(用 表示);
表示);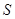 ,求
,求 ,
, ,函数
,函数 .
. 的最小正周期;(Ⅱ)若
的最小正周期;(Ⅱ)若 ,求函数
,求函数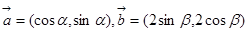 ,且
,且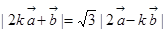 (
(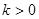 ),设
),设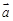 与
与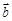 的夹角为
的夹角为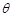
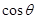 与
与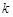 的函数关系式;
的函数关系式;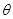 取最大值时,求
取最大值时,求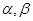 满足的关系式.
满足的关系式. .
. 的最小正周期;
的最小正周期; 中,
中, 分别是
分别是 A、
A、 ,
, ,
, ,求
,求 的值.
的值. 函数
函数

 解析式;
解析式;  的单调递减区间;
的单调递减区间; 上的图像.(要求列表、描点、连线)
上的图像.(要求列表、描点、连线)