题目内容
求函数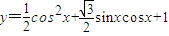
的最大值．
【答案】分析：利用两角和的正弦公式，二倍角的三角函数公式化简函数的解析式，再利用正弦函数的最大值求得函数的最大值．
解答：解：函数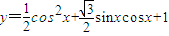
=
cos2x+
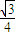sin2x+
=
sin（
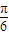+2x）+
．
故函数的最大值为
+
=
．
点评：本题考查两角和的正弦公式，二倍角的三角函数公式的应用，以及正弦函数的最大值，化简函数的解析式
是解题的关键．
解答：解：函数
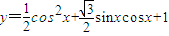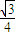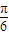=cos2x+sin2x+=sin（+2x）+．故函数的最大值为
+=．点评：本题考查两角和的正弦公式，二倍角的三角函数公式的应用，以及正弦函数的最大值，化简函数的解析式
是解题的关键．
练习册系列答案
相关题目
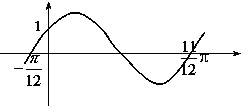已知函数y=2sin（ωx+?）（ω＞0，|?|＜