题目内容
(本小题满分14分)
在四棱锥 中,
中, //
// ,
, ,
,  ,
, 平面
平面 ,
, .
.

(Ⅰ)设平面 平面
平面 ,求证:
,求证: //
// ;
;
(Ⅱ)求证: 平面
平面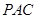 ;
;
(Ⅲ)设点 为线段
为线段 上一点,且直线
上一点,且直线 与平面
与平面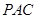 所成角的正弦值为
所成角的正弦值为 ,求
,求 的值.
的值.
在四棱锥
 中,
中, //
// ,
, ,
,  ,
, 平面
平面 ,
, .
. 
(Ⅰ)设平面
 平面
平面 ,求证:
,求证: //
// ;
;(Ⅱ)求证:
 平面
平面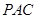 ;
;(Ⅲ)设点
 为线段
为线段 上一点,且直线
上一点,且直线 与平面
与平面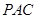 所成角的正弦值为
所成角的正弦值为 ,求
,求 的值.
的值.(1)主要根据 ,那么得到线线平行。
,那么得到线线平行。
(2)建立空间直角坐标系,然后借助于直线的方向向量和平面的法向量平行来表示证明。
(3)
 ,那么得到线线平行。
,那么得到线线平行。(2)建立空间直角坐标系,然后借助于直线的方向向量和平面的法向量平行来表示证明。
(3)

试题分析:(1)
 ,
,
又面
 ,
, ———————————4分
———————————4分(2)以
 点为坐标原点,
点为坐标原点, 为
为 轴,
轴, 轴,
轴,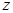 轴建立空间直角坐标系。
轴建立空间直角坐标系。则
 ————————7分
————————7分
 即
即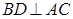
 ,即
,即 ,又
,又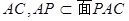
 ————————————————————————————9分
————————————————————————————9分(3)由(2)得,
 是面
是面 的一个法向量,——————————————11分
的一个法向量,——————————————11分设
 ,则
,则 ,
,
则

 ————————————————————————————————14分
————————————————————————————————14分点评:对于空间中的平行和垂直的证明,以及角的求解是立体几何重点考查的题型之一,通常可以用几何法或向量法来得到。属于中档题。

练习册系列答案
相关题目
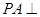 ⊙
⊙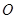 所在的平面,AB是⊙
所在的平面,AB是⊙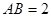 ,
,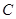 是⊙
是⊙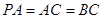 ,
,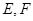 分别为
分别为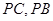 中点。
中点。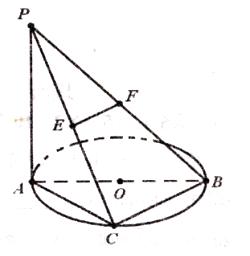
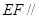 平面
平面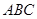 ;
;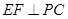 ;
;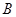 -
-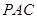 的体积。
的体积。
 中,底面
中,底面 是边长为2的菱形,
是边长为2的菱形, 是棱
是棱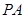 上的动点.
上的动点.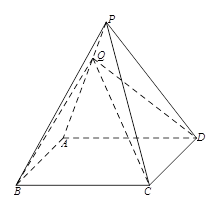
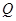 是
是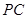 //平面
//平面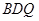 ;
;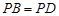 ,求证:
,求证: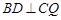 ;
;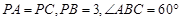 ,求四棱锥
,求四棱锥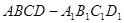 中,下列结论错误的是
中,下列结论错误的是 ∥平面
∥平面
 平面
平面

 与
与 所成的角是45º
所成的角是45º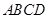 所在平面与平面
所在平面与平面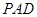 垂直,
垂直,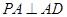 ,且
,且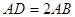 ,
,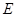 为
为 上的动点.
上的动点.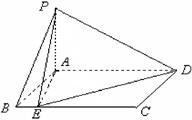
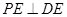 ;
;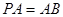 ,在线段
,在线段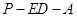 的大小为
的大小为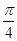 . 若存在,确定点E的位置,若不存在,说明理由.
. 若存在,确定点E的位置,若不存在,说明理由.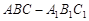 中,
中,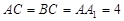 ,
, 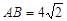 ,若
,若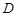 是
是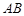 中点.
中点.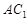 ∥平面
∥平面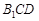 ;
; 所成的角.
所成的角.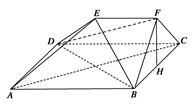
 中,
中, ,
, .
.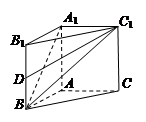
 与
与 所成的角为
所成的角为 ,求棱柱的高;
,求棱柱的高; 是
是 的中点,
的中点, 与平面
与平面 所成的角为
所成的角为 ,当棱柱的高变化时,求
,当棱柱的高变化时,求 的最大值.
的最大值.