题目内容
已知函数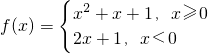 .若f(m)<f(2-m2),则实数m的取值范围是
.若f(m)<f(2-m2),则实数m的取值范围是
- A.(-∞,-1)∪(2,+∞)
- B.(-1,2)
- C.(-2,1)
- D.(-∞,-2)∪(1,+∞)
C
分析:先判断函数f(x)在在R上的单调性,然后依据单调性去掉不等式f(m)<f(2-m2)中的符号“f”,从而可解得m的范围.
解答:当x≥0时,f(x)= +
+ 单调递增;
单调递增;
当x<0时,f(x)=2x+1单调递增;
又2×0+1=1≤02+0+1=1,所以f(x)在R上单调递增,
由f(m)<f(2-m2),得m<2-m2,即m2+m-2<0,解得-2<m<1,
所以实数m的取值范围是(-2,1).
故选C.
点评:本题考查函数单调性的判断及其应用,考查学生分析问题解决问题的能力.
分析:先判断函数f(x)在在R上的单调性,然后依据单调性去掉不等式f(m)<f(2-m2)中的符号“f”,从而可解得m的范围.
解答:当x≥0时,f(x)=
 +
+ 单调递增;
单调递增;当x<0时,f(x)=2x+1单调递增;
又2×0+1=1≤02+0+1=1,所以f(x)在R上单调递增,
由f(m)<f(2-m2),得m<2-m2,即m2+m-2<0,解得-2<m<1,
所以实数m的取值范围是(-2,1).
故选C.
点评:本题考查函数单调性的判断及其应用,考查学生分析问题解决问题的能力.

练习册系列答案
相关题目
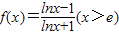 ,若f(m)+f(n)=1,则f的最小值为( )
,若f(m)+f(n)=1,则f的最小值为( )



 ,若f(m)=3,则实数m的值为 .
,若f(m)=3,则实数m的值为 . ,若f(m)+f(n)=1,则f的最小值为( )
,若f(m)+f(n)=1,则f的最小值为( )

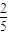

 ,若f(m)+f(n)=1,则f的最小值为 .
,若f(m)+f(n)=1,则f的最小值为 .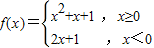 .若f(m)<f(2-m2),则实数m的取值范围是( )
.若f(m)<f(2-m2),则实数m的取值范围是( )