题目内容
已知函数 ,若f(m)+f(n)=1,则f的最小值为 .
,若f(m)+f(n)=1,则f的最小值为 .
【答案】分析:先根据函数f(x)的解析式和f(m)+f(n)=1用lnn表示出lnm,然后代入到f(mn)的表达式,最后由基本不等式可得答案.
解答:解:∵f(x)=
∴f(m)+f(n)=2- -
- =1∴
=1∴ ∴lnm+1=
∴lnm+1=
∴f(mn)=1- =1-
=1- =1-
=1- =1-
=1-
=1- ≥1-
≥1- =
= (当且仅当
(当且仅当 ,即n=m=e3时等号取到)
,即n=m=e3时等号取到)
故答案为:
点评:本题主要考查基本不等式的应用.属中档题.使用基本不等式时注意等号成立的条件.
解答:解:∵f(x)=

∴f(m)+f(n)=2-
 -
- =1∴
=1∴ ∴lnm+1=
∴lnm+1=
∴f(mn)=1-
 =1-
=1- =1-
=1- =1-
=1-
=1-
 ≥1-
≥1- =
= (当且仅当
(当且仅当 ,即n=m=e3时等号取到)
,即n=m=e3时等号取到)故答案为:

点评:本题主要考查基本不等式的应用.属中档题.使用基本不等式时注意等号成立的条件.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
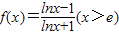 ,若f(m)+f(n)=1,则f的最小值为( )
,若f(m)+f(n)=1,则f的最小值为( )



 ,若f(m)=3,则实数m的值为 .
,若f(m)=3,则实数m的值为 . ,若f(m)+f(n)=1,则f的最小值为( )
,若f(m)+f(n)=1,则f的最小值为( )

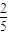

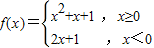 .若f(m)<f(2-m2),则实数m的取值范围是( )
.若f(m)<f(2-m2),则实数m的取值范围是( )