题目内容
已知函数f(x)=
ax2-2x-2+lnx,a∈R.
(1)当a=0时,求f(x)的单调增区间;
(2)若f(x)在(1,+∞)上只有一个极值点,求实数a的取值范围;
(3)对于任意x1,x2∈(0,1],都有|x1-x2|≤f(x1)-f(x2)|,求实数a的取值范围.
| 1 | 2 |
(1)当a=0时,求f(x)的单调增区间;
(2)若f(x)在(1,+∞)上只有一个极值点,求实数a的取值范围;
(3)对于任意x1,x2∈(0,1],都有|x1-x2|≤f(x1)-f(x2)|,求实数a的取值范围.
分析:(1)当a=0时,f(x)=-2x+2+lnx,则f′(x)=
-2,由此能求出f(x)的单调增区间.
(2)令f′(x)=ax-2+
=
=0,f(x)在(1,+∞)上只有一个极值点,故f′(x)=0在(1,+∞)上只有一个根且不是重根.令g(x)=ax2-2x+1,x∈(1,+∞).进行分类讨论能求出实数a的取值范围.
(3)当a≥1时,f′(x)=
=
,f(x)在(0,1]上单调递增.引入新函数:h(x)=f(x)-x=
ax2-3x-2+lnx,问题转化为h′(x)≥0,x∈(0,1]上恒成立,由此得到a≥
;当a<1且a≠0时
<1与|x1-x2|≤|f(x1)-f(x2)|矛盾.当a=0时,f(x)在(0,1)上只有一个极大值,同样得出矛盾.由此能求出实数a的范围.
| 1 |
| x |
(2)令f′(x)=ax-2+
| 1 |
| x |
| ax2-2x+1 |
| x |
(3)当a≥1时,f′(x)=
| ax2-2x+1 |
| x |
a(x-
| ||||
| x |
| 1 |
| 2 |
| 9 |
| 4 |
| |f(x1)-f(x2)| |
| |x1-x2| |
解答:解:(1)当a=0时,f(x)=-2x+2+lnx,
令f′(x)=
-2=
>0,
解得0<x<
.
∴f(x)的单调增区间是(0,
).
(2)∵令f′(x)=ax-2+
=
=0,
f(x)在(1,+∞)上只有一个极值点,
∴f′(x)=0在(1,+∞)上只有一个根且不是重根.
令g(x)=ax2-2x+1,x∈(1,+∞).
①当a=0时,g(x)=-2x+1,不在(1,+∞)上有一个根,舍去.
②当a>0时,g(x)=ax2-2x+1,在(1,+∞)上只有一个根,且不是重根,
∴g(1)<0,∴0<a<1;
③当a<0时,g(x)=ax2-2x+1,在(1,+∞)上只有一个根,且不是重根,
∴g(1)>0,∴a>1,矛盾.
综上所述,实数a的取值值范围是:0<a<1.
(3)当x1=x2时,满足条件.以下以讨论x1≠x2的情况.
①当a≥1时,f′(x)=
=
,
∵x∈(0,1],
∈(0,1],
∴a(x-
) 2-
+1≥1-
≥0,
得到f′(x)≥0,
即f(x)在(0,1]上单调递增.
对于任意x1,x2∈(0,1],设x1<x2,则有f(x1)<f(x2),代入不等式:
|x1-x2|≤|f(x1)-f(x2)|,
∴f(x2)-f(x1)≥x2-x1,
∴f(x2)-x2≥f(x1)-x1.
引入新函数:h(x)=f(x)-x=
ax2-3x-2+lnx,
h′(x)=ax-3+
=
,
∴问题转化为h′(x)≥0,x∈(0,1]上恒成立,
∴ax2-3x+1≥0,
∴a≥
,
∴a≥ (
)max,
令l(x)=
,
∵l′(x)=
,
∴当0<x<
时,l′(x)>0;
当
<x<1时,l′(x)<0.
∴x=
时,l(x)min=l(
)=
,
∴a≥
.
②当a<1且a≠0时,f′(x)=
,
令k(x)=ax2-2x+1=0,
方程判别式△=4-4>0,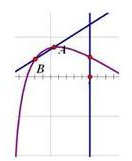
且k(1)=a-1<0.
∴f(x)在(0,1)上只有一个极大值.
设极大值点为x1,记A(x1,f(x1)),在点A处的斜率为0;
过A点作一条割线AB,肯定存在点B(x2,f(x2)),
使|kAB|<1.
∵|kAB|慢慢变成0,
这样存在x1,x2,
使得
<1与|x1-x2|≤|f(x1)-f(x2)|矛盾.
当a=0时,f(x)在(0,1)上只有一个极大值,同样得出矛盾.
综上所述,实数a的范围是{a|a≥
}.
令f′(x)=
| 1 |
| x |
| 1-2x |
| x |
解得0<x<
| 1 |
| 2 |
∴f(x)的单调增区间是(0,
| 1 |
| 2 |
(2)∵令f′(x)=ax-2+
| 1 |
| x |
| ax2-2x+1 |
| x |
f(x)在(1,+∞)上只有一个极值点,
∴f′(x)=0在(1,+∞)上只有一个根且不是重根.
令g(x)=ax2-2x+1,x∈(1,+∞).
①当a=0时,g(x)=-2x+1,不在(1,+∞)上有一个根,舍去.
②当a>0时,g(x)=ax2-2x+1,在(1,+∞)上只有一个根,且不是重根,
∴g(1)<0,∴0<a<1;
③当a<0时,g(x)=ax2-2x+1,在(1,+∞)上只有一个根,且不是重根,
∴g(1)>0,∴a>1,矛盾.
综上所述,实数a的取值值范围是:0<a<1.
(3)当x1=x2时,满足条件.以下以讨论x1≠x2的情况.
①当a≥1时,f′(x)=
| ax2-2x+1 |
| x |
a(x-
| ||||
| x |
∵x∈(0,1],
| 1 |
| a |
∴a(x-
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
得到f′(x)≥0,
即f(x)在(0,1]上单调递增.
对于任意x1,x2∈(0,1],设x1<x2,则有f(x1)<f(x2),代入不等式:
|x1-x2|≤|f(x1)-f(x2)|,
∴f(x2)-f(x1)≥x2-x1,
∴f(x2)-x2≥f(x1)-x1.
引入新函数:h(x)=f(x)-x=
| 1 |
| 2 |
h′(x)=ax-3+
| 1 |
| x |
| ax2-3x+1 |
| x |
∴问题转化为h′(x)≥0,x∈(0,1]上恒成立,
∴ax2-3x+1≥0,
∴a≥
| 3x-1 |
| x2 |
∴a≥ (
| 3x-1 |
| x2 |
令l(x)=
| 3x-1 |
| x2 |
∵l′(x)=
| 2-3x |
| x3 |
∴当0<x<
| 2 |
| 3 |
当
| 2 |
| 3 |
∴x=
| 2 |
| 3 |
| 2 |
| 3 |
| 9 |
| 4 |
∴a≥
| 9 |
| 4 |
②当a<1且a≠0时,f′(x)=
| ax2-2x+1 |
| x |
令k(x)=ax2-2x+1=0,
方程判别式△=4-4>0,

且k(1)=a-1<0.
∴f(x)在(0,1)上只有一个极大值.
设极大值点为x1,记A(x1,f(x1)),在点A处的斜率为0;
过A点作一条割线AB,肯定存在点B(x2,f(x2)),
使|kAB|<1.
∵|kAB|慢慢变成0,
这样存在x1,x2,
使得
| |f(x1)-f(x2)| |
| |x1-x2| |
当a=0时,f(x)在(0,1)上只有一个极大值,同样得出矛盾.
综上所述,实数a的范围是{a|a≥
| 9 |
| 4 |
点评:本题考查利用导数求函数最值的应用,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)=
,g(x)=1+
,若f(x)>g(x),则实数x的取值范围是( )
| 1 |
| |x| |
| x+|x| |
| 2 |
| A、(-∞,-1)∪(0,1) | ||||
B、(-∞,-1)∪(0,
| ||||
C、(-1,0)∪(
| ||||
D、(-1,0)∪(0,
|