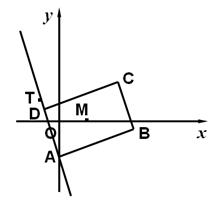
题目内容
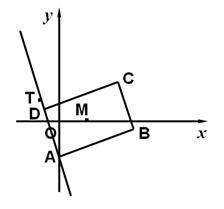
如图,矩形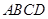 的两条对角线相交于点
的两条对角线相交于点 ,
,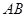 边所在直线的方程为
边所在直线的方程为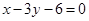 点
点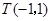 在
在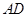 边所在直线上.
边所在直线上.
(I)求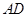 边所在直线的方程;
边所在直线的方程;
(II)求矩形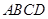 外接圆的方程;
外接圆的方程;
(III)若动圆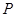 过点
过点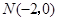 ,且与矩形
,且与矩形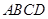 的外接圆外切,求动圆
的外接圆外切,求动圆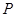 的圆心的轨迹方程.
的圆心的轨迹方程.
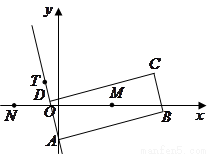
【答案】
(I)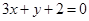 .
.
(II)矩形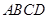 外接圆的方程为
外接圆的方程为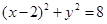 .
.
(III)动圆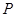 的圆心的轨迹方程为
的圆心的轨迹方程为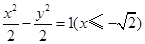
【解析】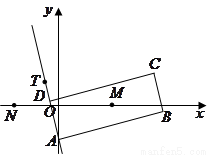 解:(I)因为
解:(I)因为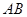 边所在直线的方程为
边所在直线的方程为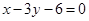 ,且
,且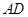 与
与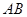 垂直,所以直线
垂直,所以直线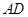 的斜率为
的斜率为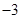 .
.
又因为点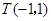 在直线
在直线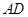 上,
上,
所以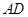 边所在直线的方程为
边所在直线的方程为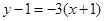 .
.
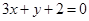 .
.
(II)由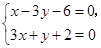 解得点
解得点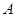 的坐标为
的坐标为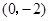 ,
,
因为矩形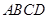 两条对角线的交点为
两条对角线的交点为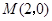 .
.
所以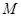 为矩形
为矩形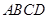 外接圆的圆心.
外接圆的圆心.
又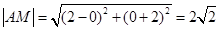 .
.
从而矩形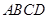 外接圆的方程为
外接圆的方程为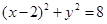 .
.
(III)因为动圆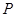 过点
过点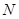 ,所以
,所以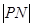 是该圆的半径,又因为动圆
是该圆的半径,又因为动圆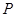 与圆
与圆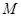 外切,
外切,
所以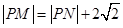 ,
,
即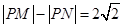 .
.
故点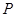 的轨迹是以
的轨迹是以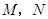 为焦点,实轴长为
为焦点,实轴长为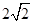 的双曲线的左支.
的双曲线的左支.
因为实半轴长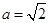 ,半焦距
,半焦距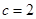 .
.
所以虚半轴长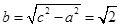 .
.
从而动圆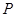 的圆心的轨迹方程为
的圆心的轨迹方程为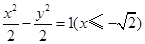

练习册系列答案
相关题目
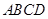 的两条对角线相交于点
的两条对角线相交于点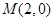 ,
,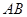 边所在直线的方程为
边所在直线的方程为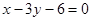 ,点
,点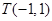 在
在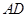 边所在直线上。
边所在直线上。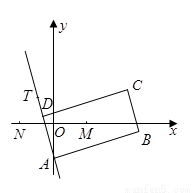
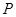 过点
过点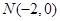 ,且与矩形
,且与矩形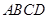 的两条对角线相交于点
的两条对角线相交于点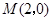 ,
,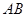 边所在直线的方程为
边所在直线的方程为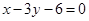 点
点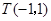 在
在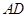 边所在直线上.
边所在直线上.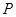 过点
过点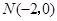 ,且与矩形
,且与矩形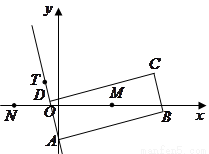
 的两条对角线相交于点
的两条对角线相交于点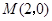 ,
,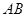 边所在直线的方程为
边所在直线的方程为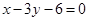 , 点
, 点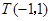 在
在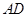 边所在直线上.求:
边所在直线上.求: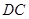 边所在的直线方程.
边所在的直线方程.
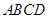 的两条对角线相交于点
的两条对角线相交于点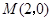 ,
,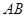 边所在直线的方程为
边所在直线的方程为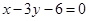 , 点
, 点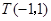 在
在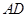 边所在直线上.求:
边所在直线上.求: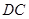 边所在的直线方程.
边所在的直线方程.