题目内容
设函数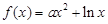 .
.
(1)求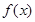 的单调区间;
的单调区间;
(2)设函数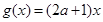 ,若当
,若当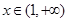 时,
时,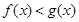 恒成立,求
恒成立,求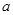 的取值范围.
的取值范围.
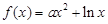 .
. (1)求
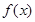 的单调区间;
的单调区间;(2)设函数
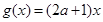 ,若当
,若当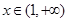 时,
时,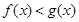 恒成立,求
恒成立,求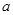 的取值范围.
的取值范围.(1) 当 时,
时,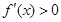 ,所以
,所以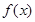 在
在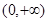 上是增函数当
上是增函数当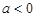 时,
时,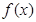 在
在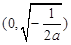 上是增函数,在
上是增函数,在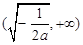 上是减函数;(2)
上是减函数;(2)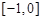
 时,
时,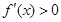 ,所以
,所以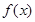 在
在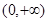 上是增函数当
上是增函数当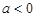 时,
时,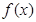 在
在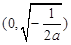 上是增函数,在
上是增函数,在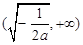 上是减函数;(2)
上是减函数;(2)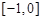
试题分析:(1)根据导数公式求出
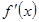 ,对于含有的参数
,对于含有的参数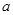 要进行讨论,
要进行讨论,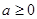 或
或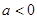 两种情况;(2)设
两种情况;(2)设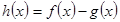 ,将
,将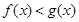 恒成立,转化成
恒成立,转化成 恒成立,所以求
恒成立,所以求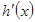 ,将
,将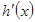 分解因式,讨论
分解因式,讨论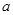 的范围,确定
的范围,确定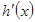 的正负,讨论
的正负,讨论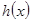 的单调性,确定
的单调性,确定 恒成立的条件,确定
恒成立的条件,确定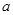 的范围,此题考察了导数的应用,属于中等偏上的系统,两问都考察到了分类讨论
的范围,此题考察了导数的应用,属于中等偏上的系统,两问都考察到了分类讨论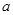 的范围,这是我们在做题时考虑问题不全面,容易丢分的环节.
的范围,这是我们在做题时考虑问题不全面,容易丢分的环节.试题解析:(1)解:因为
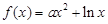 ,其中
,其中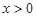 . 所以
. 所以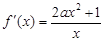 , 2分
, 2分当
 时,
时,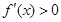 ,所以
,所以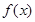 在
在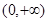 上是增函数 4分
上是增函数 4分当
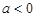 时,令
时,令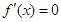 ,得
,得
所以
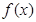 在
在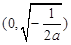 上是增函数,在
上是增函数,在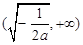 上是减函数. 6分
上是减函数. 6分(2)解:令
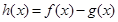 ,则
,则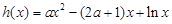 ,
,根据题意,当
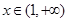 时,
时,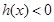 恒成立. 8分
恒成立. 8分所以
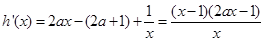
(1)当
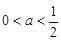 时,
时,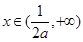 时,
时,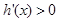 恒成立.
恒成立.所以
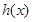 在
在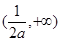 上是增函数,且
上是增函数,且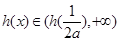 ,所以不符题意 10分
,所以不符题意 10分(2)当
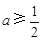 时,
时,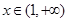 时,
时,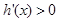 恒成立.
恒成立.所以
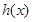 在
在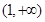 上是增函数,且
上是增函数,且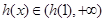 ,所以不符题意 12分
,所以不符题意 12分(3)当
 时,
时,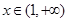 时,恒有
时,恒有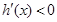 ,故
,故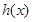 在
在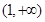 上是减函数,
上是减函数,于是“
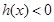 对任意
对任意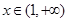 都成立”的充要条件是
都成立”的充要条件是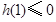 ,
, 即
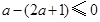 ,解得
,解得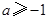 ,故
,故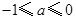 .
.综上所述,
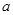 的取值范围是
的取值范围是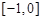 . 15分
. 15分
练习册系列答案
相关题目
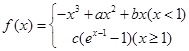 在
在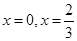 处存在极值.
处存在极值.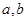 的值;
的值;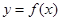 的图像上存在两点A,B使得
的图像上存在两点A,B使得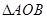 是以坐标原点O为直角顶点的直角三角形,且斜边AB的中点在
是以坐标原点O为直角顶点的直角三角形,且斜边AB的中点在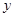 轴上,求实数
轴上,求实数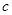 的取值范围;
的取值范围;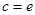 时,讨论关于
时,讨论关于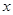 的方程
的方程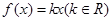 的实根个数.
的实根个数.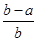 <ln
<ln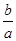 <
<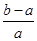 ,其中0<a<b;
,其中0<a<b;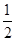 + +
+ +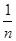 ]≤1+[lnn](n∈N*).
]≤1+[lnn](n∈N*).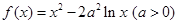 .
.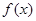 的单调区间;
的单调区间;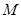 ,求证:
,求证: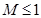 .
.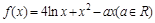 .
.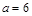 时,求函数
时,求函数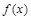 的单调区间;
的单调区间;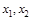 ,且
,且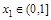 ,求证:
,求证: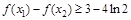 ;
;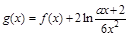 ,对于任意
,对于任意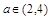 时,总存在
时,总存在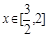 ,使
,使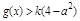 成立,求实数
成立,求实数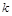 的取值范围.
的取值范围.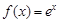 ,
,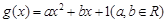 .
.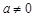 ,则
,则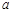 ,
,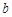 满足什么条件时,曲线
满足什么条件时,曲线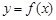 与
与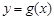 在
在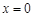 处总有相同的切线?
处总有相同的切线?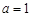 时,求函数
时,求函数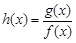 的单调减区间;
的单调减区间;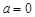 时,若
时,若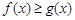 对任意的
对任意的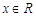 恒成立,求
恒成立,求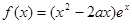 ,其中
,其中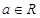 ,曲线
,曲线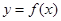 在点
在点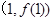 处的切线垂直于
处的切线垂直于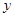 轴.
轴.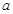 的值;
的值;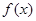 的极值.
的极值.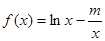 (
(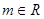 )在区间
)在区间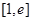 上取得最小值4,则
上取得最小值4,则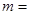 _ __.
_ __.