题目内容
下列命题中,真命题是
①?x0∈R,ex0≤0
②?x∈R,2x>x2
③a>1,b>1是ab>1的充分条件
④b=
是a,b,c成等比的既不充分又不必要条件.
③、④
③、④
(写出所有真命题的序号).①?x0∈R,ex0≤0
②?x∈R,2x>x2
③a>1,b>1是ab>1的充分条件
④b=
| ac |
分析:①根据指数函数的性质可判断①
②当x=2时可知,2x=x2成立可判断②
③当a>1,b>1时,根据不等式的性质可知ab>1,
④当b=a=0时,满足b=
但a,b,c不成等比;当a,b,c成等比数列,但是当a=1,b=-2,c=4时,不满足b=
,
②当x=2时可知,2x=x2成立可判断②
③当a>1,b>1时,根据不等式的性质可知ab>1,
④当b=a=0时,满足b=
| ac |
| ac |
解答:解:①根据指数函数的性质可知,?x0∈R,ex0≤0为假命题
②当x=2时可知,2x=x2成立可知,?x∈R,2x>x2为假命题
③当a>1,b>1时,根据不等式的性质可知ab>1,则可得a>1,b>1是ab>1的充分条件为真命题
④当b=a=0时,满足b=
但a,b,c不成等比
当a,b,c成等比数列,但是当a=1,b=-2,c=4时,不满足b=
,即b=
是a,b,c成等比的既不充分又不必要条件为真命题
正确的命题有③④
故答案为:③④
②当x=2时可知,2x=x2成立可知,?x∈R,2x>x2为假命题
③当a>1,b>1时,根据不等式的性质可知ab>1,则可得a>1,b>1是ab>1的充分条件为真命题
④当b=a=0时,满足b=
| ac |
当a,b,c成等比数列,但是当a=1,b=-2,c=4时,不满足b=
| ac |
| ac |
正确的命题有③④
故答案为:③④
点评:本题以命题的真假判断为载体,主要考查了指数函数与二次函数的性质的应用,不等式的性质及等比数列的性质的综合考查

练习册系列答案
相关题目
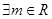 ,使函数
,使函数 是偶函数
是偶函数 ,使函数
,使函数 ≤0
≤0 =-1
=-1