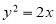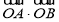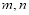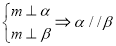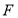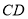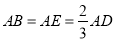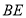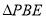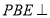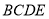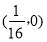题目内容
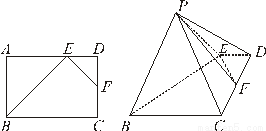
在正四棱锥P-ABCD中,PA=2,直线PA与平面ABCD所成角为60°,E为PC的中点,则异面直线PA与BE所成角为( )
A. B.
B.
 C.
C.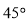 D.
D.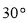
C
【解析】
试题分析:连接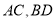 交于点
交于点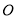 ,连接
,连接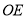 ,
,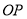 。因为
。因为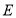 为
为 中点,所以
中点,所以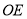 ∥
∥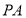 ,所以
,所以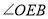 即为异面直线
即为异面直线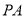 与
与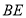 所成的角。因为四棱锥
所成的角。因为四棱锥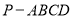 为正四棱锥,所以
为正四棱锥,所以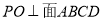 ,所以
,所以 为
为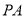 在面
在面 内的射影,所以
内的射影,所以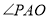 即为
即为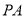 与面
与面 所成的角,即
所成的角,即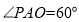 ,因为
,因为 ,所以
,所以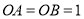 ,
, 。所以在直角三角形
。所以在直角三角形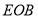 中
中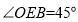 ,即面直线
,即面直线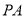 与
与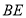 所成的角为
所成的角为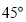 。
。
考点:1异面直线所成角;2线面角;3线面垂直。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目