题目内容
设A={x|x2+4x=0},B={x|x2+2(a+1)x+a2-1=0},其中x∈R,如果A∩B=B,求实数a的取值范围.
a=1或a≤-1
解析试题分析:A={0,-4},又A∩B=B,所以B⊆A. 3分
(1)B=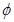 时,Δ=4(a+1)2-4(a2-1)<0,得a<-1; 4分
时,Δ=4(a+1)2-4(a2-1)<0,得a<-1; 4分
(2)B={0}或B={-4}时, 5分
把x=0代入x2+2(a+1)x+a2-1=0中得a=±1,
把x=-4代入x2+2(a+1)x+a2-1=0,
得a=1或7,又因为Δ=0,得a=-1; 8分
(3)B={0,-4}时,Δ=a+1>0,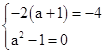 ,解得a=1.
,解得a=1.
综上所述实数a=1或a≤-1. 12分
考点:本题考查了集合的关系及运算
点评:解答此类问题要注意以下几点:①解决集合与函数的综合问题时,要注意灵活运用集合的相关知识,掌握函数值域、定义域的求法及图象与性质的应用;②要充分利用数形结合的思想方法;③要弄清集合中元素是什么?(自变量值x、函数值y还是图象的点);④对于含参数的函数问题,一般需要对参数进行讨论,要特别注意检验集合的元素是否满足“三性”,还要提防“空集”这一隐性陷阱.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
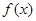 =
=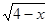
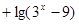 的定义域为
的定义域为 ,集合
,集合 =
= ,
, ,求
,求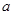 的取值范围.
的取值范围.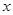 的不等式
的不等式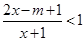 的解集
的解集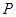 ,不等式
,不等式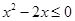 的解集为
的解集为 .
.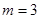 ,求集合
,求集合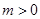 且
且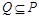 ,求
,求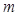 的取值范围.
的取值范围. ,
,
 ,求实数
,求实数 的值;
的值;  ,求实数
,求实数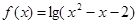 的定义域为集合A,函数
的定义域为集合A,函数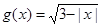 的定义域为集合B.
的定义域为集合B.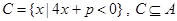 ,求实数
,求实数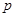 的取值范围.
的取值范围.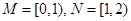 ,函数
,函数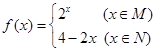 .
.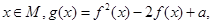 且
且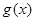 的最小值为1;求实数
的最小值为1;求实数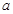 的值
的值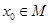 ,且
,且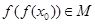 ,求
,求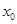 的取值范围.
的取值范围.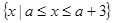 ,B=
,B=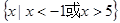 .
.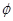 ,求实数a的取值范围;
,求实数a的取值范围;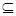 B,求实数a的取值范围.
B,求实数a的取值范围. ,若
,若 ,则称
,则称 为
为 ,则称
,则称
 ,若
,若 上单调递增函数,是否有
上单调递增函数,是否有 ?若是,请证明。
?若是,请证明。 表示集合
表示集合 中元素的个数,问:
中元素的个数,问: 若函数
若函数 ,若
,若 ,则
,则 是否等于0?若是,请证明
是否等于0?若是,请证明 若
若 ,试问:
,试问: 是否一定等于1?若是,请证明
是否一定等于1?若是,请证明