题目内容
抛物线y=ax2与直线y=kx+b(k≠0)交于A、B两点,且此两点的横坐标分别为x1、x2,直线与x轴的交点的横坐标是x3,则恒有
[ ]
A.
x3=x1+x2
B.
x1x2=x1x3+x2x3
C.
x1+x2+x3=0
D.
x1x2+x2x3+x3x1=0
答案:B
解析:
解析:
|
解方程组 ax2-kx-b=0,由韦达定理及题设得 x3(x1+x2)=x1x2,即x1x2=x1x3+x2x3. |

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
 得
得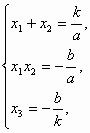 由
由