题目内容
已知函数 ,(x>0).
,(x>0).(Ⅰ)当0<a<b,且f(a)=f(b)时,求证:ab>1;
(Ⅱ)是否存在实数a,b(a<b),使得函数y=f(x)的定义域、值域都是[a,b],若存在,则求出a,b的值,若不存在,请说明理由.
(Ⅲ)若存在实数a,b(a<b),使得函数y=f(x)的定义域为[a,b]时,值域为[ma,mb](m≠0),求m的取值范围.
【答案】分析:(I)确定函数解析式,利用函数的单调性,可得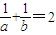 ,利用基本不等式,即可得出结论;
,利用基本不等式,即可得出结论;
(II)分类讨论,若存在满足条件的实数a,b,使得函数y=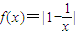 的定义域、值域都是[a,b],从而可得结论;
的定义域、值域都是[a,b],从而可得结论;
(III)分类讨论,若存在实数a,b(a<b),使得函数y=f(x)的定义域为[a,b]时,值域为[ma,mb],即可得出结论.
解答:(I)证明:∵x>0,∴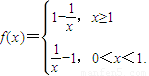
∴f(x)在(0,1)上为减函数,在(1,+∞)上是增函数.
由0<a<b,且f(a)=f(b),可得 0<a<1<b和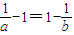 ,即
,即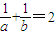 .
.
∴2ab=a+b>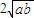 .…(3分)
.…(3分)
故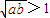 ,即ab>1.…(4分)
,即ab>1.…(4分)
(II)解:不存在满足条件的实数a,b.
若存在满足条件的实数a,b,使得函数y=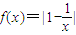 的定义域、值域都是[a,b],
的定义域、值域都是[a,b],
则a>0,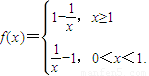
①当a,b∈(0,1)时,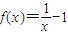 在(0,1)上为减函数.
在(0,1)上为减函数.
故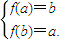 ,即
,即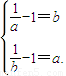 ,解得a=b.
,解得a=b.
故此时不存在适合条件的实数a,b.…(6分)
②当a,b∈[1,+∞)时,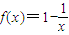 在(1,+∞)上是增函数.
在(1,+∞)上是增函数.
故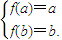 ,即
,即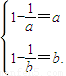
此时a,b是方程x2-x+1=0的根,此方程无实根.
故此时不存在适合条件的实数a,b.…(8分)
③当a∈(0,1),b∈[1,+∞)时,由于1∈[a,b],而f(1)=0∉[a,b],
故此时不存在适合条件的实数a,b.
综上可知,不存在适合条件的实数a,b.…(10分)
(III)若存在实数a,b(a<b),使得函数y=f(x)的定义域为[a,b]时,值域为[ma,mb].
则a>0,m>0.
①当a,b∈(0,1)时,由于f(x)在(0,1)上是减函数,故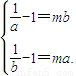 .
.
此时刻得a,b异号,不符合题意,所以a,b不存在.
②当a∈(0,1)或b∈[1,+∞)时,由( II)知0在值域内,值域不可能是[ma,mb],所以a,b不存在.
故只有a,b∈[1,+∞).
∵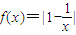 在[1,+∞)上是增函数,
在[1,+∞)上是增函数,
∴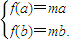 ,即
,即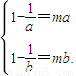
∴a,b是方程mx2-x+1=0的两个根,即关于x的方程mx2-x+1=0有两个大于1的实根.…(12分)
设这两个根为x1,x2,则x1+x2=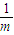 ,x1•x2=
,x1•x2=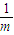 .
.
∴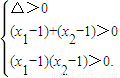 ,即
,即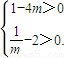
解得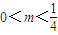 .
.
故m的取值范围是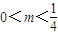 .…(14分)
.…(14分)
点评:本题考查函数解析式的运用,考查基本不等式,考查分类讨论的数学思想,考查学生分析解决问题的能力,属于中档题.
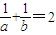 ,利用基本不等式,即可得出结论;
,利用基本不等式,即可得出结论;(II)分类讨论,若存在满足条件的实数a,b,使得函数y=
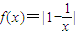 的定义域、值域都是[a,b],从而可得结论;
的定义域、值域都是[a,b],从而可得结论;(III)分类讨论,若存在实数a,b(a<b),使得函数y=f(x)的定义域为[a,b]时,值域为[ma,mb],即可得出结论.
解答:(I)证明:∵x>0,∴
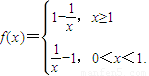
∴f(x)在(0,1)上为减函数,在(1,+∞)上是增函数.
由0<a<b,且f(a)=f(b),可得 0<a<1<b和
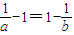 ,即
,即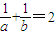 .
.∴2ab=a+b>
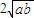 .…(3分)
.…(3分)故
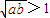 ,即ab>1.…(4分)
,即ab>1.…(4分)(II)解:不存在满足条件的实数a,b.
若存在满足条件的实数a,b,使得函数y=
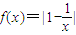 的定义域、值域都是[a,b],
的定义域、值域都是[a,b],则a>0,
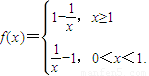
①当a,b∈(0,1)时,
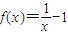 在(0,1)上为减函数.
在(0,1)上为减函数.故
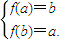 ,即
,即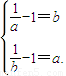 ,解得a=b.
,解得a=b.故此时不存在适合条件的实数a,b.…(6分)
②当a,b∈[1,+∞)时,
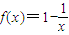 在(1,+∞)上是增函数.
在(1,+∞)上是增函数.故
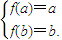 ,即
,即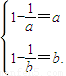
此时a,b是方程x2-x+1=0的根,此方程无实根.
故此时不存在适合条件的实数a,b.…(8分)
③当a∈(0,1),b∈[1,+∞)时,由于1∈[a,b],而f(1)=0∉[a,b],
故此时不存在适合条件的实数a,b.
综上可知,不存在适合条件的实数a,b.…(10分)
(III)若存在实数a,b(a<b),使得函数y=f(x)的定义域为[a,b]时,值域为[ma,mb].
则a>0,m>0.
①当a,b∈(0,1)时,由于f(x)在(0,1)上是减函数,故
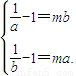 .
.此时刻得a,b异号,不符合题意,所以a,b不存在.
②当a∈(0,1)或b∈[1,+∞)时,由( II)知0在值域内,值域不可能是[ma,mb],所以a,b不存在.
故只有a,b∈[1,+∞).
∵
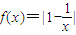 在[1,+∞)上是增函数,
在[1,+∞)上是增函数,∴
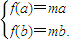 ,即
,即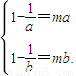
∴a,b是方程mx2-x+1=0的两个根,即关于x的方程mx2-x+1=0有两个大于1的实根.…(12分)
设这两个根为x1,x2,则x1+x2=
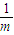 ,x1•x2=
,x1•x2=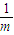 .
.∴
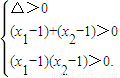 ,即
,即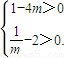
解得
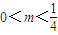 .
.故m的取值范围是
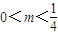 .…(14分)
.…(14分)点评:本题考查函数解析式的运用,考查基本不等式,考查分类讨论的数学思想,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
 已知函数
已知函数