题目内容
函数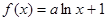
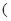
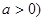 .
.
(Ⅰ) 当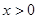 时,求证:
时,求证: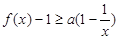 ;(4分)
;(4分)
(Ⅱ) 在区间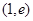 上
上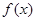
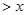 恒成立,求实数
恒成立,求实数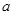 的范围。(4分)
的范围。(4分)
(Ⅲ) 当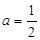 时,求证:
时,求证: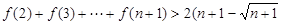 )
)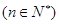 .(4分)
.(4分)
【答案】
(I)见解析(II)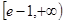 . (III)见解析
. (III)见解析
【解析】(Ⅰ)构造函数,然后利用导数法研究单调性,进一步得到不等关系;(Ⅱ)把恒成立问题转化为求函数的最值问题,然后利用导数法求解;(Ⅲ)利用放缩法证明不等式
(I)证明:设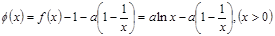
则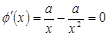 ,则
,则 ,即
,即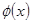 在
在 处取到最小值,
处取到最小值,
则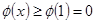 ,即原结论成立.
,即原结论成立.
(II)解:由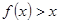 得
得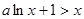 即
即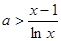 ,另
,另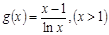 ,
,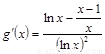
另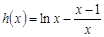 ,
, 则
则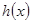 单调递增,所以
单调递增,所以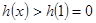
因为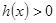 ,所以
,所以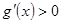 ,即
,即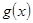 单调递增,则
单调递增,则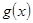 的最大值为
的最大值为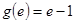
所以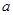 的取值范围为
的取值范围为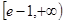 .
.
(III)证明:由第一问得知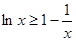 则
则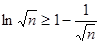
则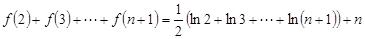
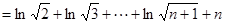
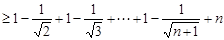
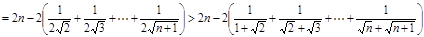
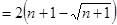

练习册系列答案
相关题目