题目内容
7.设偶函数f(x)在[0,+∞)单调递增,则使得f(x)>f(2x-1)成立的x的取值范围是( )| A. | ($\frac{1}{3}$,1) | B. | (-∞,$\frac{1}{3}$)∪(1,+∞) | C. | (-$\frac{1}{3}$,$\frac{1}{3}$) | D. | (-∞,-$\frac{1}{3}$)∪($\frac{1}{3}$,+∞) |
分析 利用偶函数的性质、单调性去掉不等式中的符号“f”,转化为具体不等式即可求解.
解答 解:因为f(x)为偶函数,
所以f(x)>f(2x-1)可化为f(|x|)>f(|2x-1|)
又f(x)在区间[0,+∞)上单调递增,所以|x|>|2x-1|,
即(2x-1)2<x2,解得$\frac{1}{3}$<x<1,
所以x的取值范围是($\frac{1}{3}$,1),
故选:A.
点评 本题考查函数的奇偶性、单调性及其应用,考查抽象不等式的求解,考查学生灵活运用知识解决问题的能力.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
2.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{2}$|$\overrightarrow{a}$|=$\sqrt{2}$|$\overrightarrow{b}$|,则向量$\overrightarrow{a}$与$\overrightarrow{a}$+$\overrightarrow{b}$夹角的余弦值为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | -$\frac{\sqrt{2}}{2}$ | C. | 0 | D. | 1 |
12.根据图1所示的程序,得到了y与x的函数图象,如图2.若点M是y轴正半轴上任意一点,过点M作PQ∥x轴交图象于点P,Q,连接OP,OQ.则以下结论:
①x<0 时,y=$\frac{2}{x}$
②△OPQ的面积为定值.
③x>0时,y随x的增大而增大.
④MQ=2PM.
⑤∠POQ可以等于90°.其中正确结论是( )
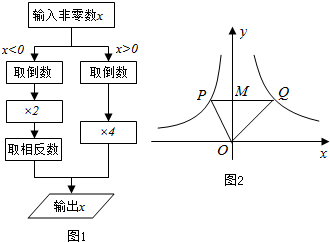
①x<0 时,y=$\frac{2}{x}$
②△OPQ的面积为定值.
③x>0时,y随x的增大而增大.
④MQ=2PM.
⑤∠POQ可以等于90°.其中正确结论是( )

| A. | ①②④ | B. | ②④⑤ | C. | ③④⑤ | D. | ②③⑤ |
19.已知函数y=f(x)(x∈R)的图象过点(1,0),f′(x)为函数f(x)的导函数,e为自然对数的底数,若x>0,xf′(x)>1下恒成立,则不等式f(x)≤lnx的解集为( )
| A. | (0,$\frac{1}{e}$] | B. | (0,1] | C. | (0,e] | D. | (1,e] |