题目内容
| |=1,|
|=1,| |=
|= ,
, •
• =0,点C在∠AOB内,且∠AOC=30°,设
=0,点C在∠AOB内,且∠AOC=30°,设 =m
=m +n
+n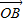 (m、n∈R),则
(m、n∈R),则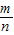 等于( )
等于( )A.

B.3
C.

D.
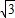
【答案】分析:将向量 沿
沿 与
与 方向利用平行四边形原则进行分解,构造出三角形,由题目已知,可得三角形中三边长及三个角,然后利用正弦定理解三角形即可得到答案.此题如果没有点C在∠AOB内的限制,应该有两种情况,即也可能为OC在OA顺时针方向30°角的位置,请大家注意分类讨论,避免出错.
方向利用平行四边形原则进行分解,构造出三角形,由题目已知,可得三角形中三边长及三个角,然后利用正弦定理解三角形即可得到答案.此题如果没有点C在∠AOB内的限制,应该有两种情况,即也可能为OC在OA顺时针方向30°角的位置,请大家注意分类讨论,避免出错.
解答: 解:法一:如图所示:
解:法一:如图所示: =
=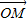 +
+ ,设
,设 =x,则
=x,则 =
=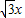 .
. =
=
∴ =
= =3.
=3.
法二:如图所示,建立直角坐标系.
则 =(1,0),
=(1,0), =(0,
=(0, ),
),
∴ =m
=m +n
+n
=(m, n),
n),
∴tan30°= =
= ,
,
∴ =3.
=3.
故选B
点评:对一个向量根据平面向量基本定理进行分解,关键是要根据平行四边形法则,找出向量在基底两个向量方向上的分量,再根据已知条件构造三角形,解三角形即可得到分解结果.
 沿
沿 与
与 方向利用平行四边形原则进行分解,构造出三角形,由题目已知,可得三角形中三边长及三个角,然后利用正弦定理解三角形即可得到答案.此题如果没有点C在∠AOB内的限制,应该有两种情况,即也可能为OC在OA顺时针方向30°角的位置,请大家注意分类讨论,避免出错.
方向利用平行四边形原则进行分解,构造出三角形,由题目已知,可得三角形中三边长及三个角,然后利用正弦定理解三角形即可得到答案.此题如果没有点C在∠AOB内的限制,应该有两种情况,即也可能为OC在OA顺时针方向30°角的位置,请大家注意分类讨论,避免出错.解答:
 解:法一:如图所示:
解:法一:如图所示: =
=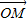 +
+ ,设
,设 =x,则
=x,则 =
=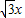 .
. =
=
∴
 =
= =3.
=3.法二:如图所示,建立直角坐标系.
则
 =(1,0),
=(1,0), =(0,
=(0, ),
),∴
 =m
=m +n
+n
=(m,
 n),
n),∴tan30°=
 =
= ,
,∴
 =3.
=3.故选B
点评:对一个向量根据平面向量基本定理进行分解,关键是要根据平行四边形法则,找出向量在基底两个向量方向上的分量,再根据已知条件构造三角形,解三角形即可得到分解结果.

练习册系列答案
相关题目
若平面向量
与向量
=(1,-2)的夹角是180°,且|
|=3
,则
=( )
| b |
| a |
| b |
| 5 |
| b |
| A、(-3,6) |
| B、(3,-6) |
| C、(6,-3) |
| D、(-6,3) |