题目内容
不等式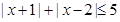 的解集为 .
的解集为 .
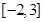
解析试题分析:由绝对值的几何意义,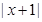 表示数轴上点
表示数轴上点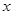 到点
到点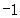 的距离,
的距离,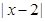 表示数轴上点
表示数轴上点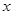 到点
到点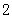 的距离,
的距离,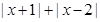 表示数轴上点
表示数轴上点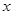 到点
到点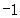 、点
、点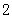 的距离之和;
的距离之和;
结合数轴不难看出,不等式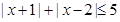 的解集为
的解集为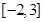 .
.
本题也可以利用“分区间讨论法”.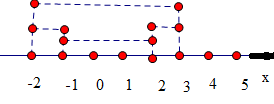
考点:绝对值的几何意义,绝对值不等式的解法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
(5分)(2011•广东)不等式2x2﹣x﹣1>0的解集是( )
A. | B.(1,+∞) | C.(﹣∞,1)∪(2,+∞) | D. ∪(1,+∞) ∪(1,+∞) |
不等式 的解集为( )
的解集为( )
A. | B. | C. | D. |
不等式(x-1)(2-x)>0的解集是( )
| A.(-∞,1) | B.(2,+∞) |
C.(-∞,1) (2,+∞) (2,+∞) | D.(1,2) |
不等式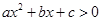 的解集为(-
的解集为(- ,2),则不等式
,2),则不等式 的解集为( )
的解集为( )
A.( ,+∞)∪(-∞,-2) ,+∞)∪(-∞,-2) |
B.(-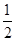 ,+∞)∪(-∞,-3) ,+∞)∪(-∞,-3) |
C.(-2, ) ) |
D.(-3,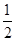 ) ) |
不等式2x -x-1>0的解集是
-x-1>0的解集是
A.( ,1) ,1) |
| B.(1,+∞) |
| C.(-∞,1)∪(2,+∞) |
D.(-∞, )∪(1,+∞) )∪(1,+∞) |
已知 ,则“
,则“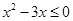 ”是“
”是“ 成立”的( )
成立”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
[2014·皖南八校联考]不等式x2-2x+5≥a2-3a对任意实数x恒成立,则实数a的取值范围为( )
| A.[-1,4] |
| B.(-∞,-2]∪[5,+∞) |
| C.(-∞,-1]∪[4,+∞) |
| D.[-2,5] |
不等式 的解集是( )
的解集是( )
A.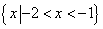 |
B. |
C.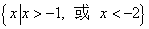 |
D. |