题目内容
8、观察下列几个三角恒等式:
①tan10°tan20°+tan20°tan60°+tan60°tan10°=1;
②tan5°tan100°+tan100°tan(-15°)+tan(-15°)tan5°=1;
③tan13°tan35°+tan35°tan42°+tan42°tan13°=1.
一般地,若tanα,tanβ,tanγ都有意义,你从这三个恒等式中猜想得到的一个结论为
①tan10°tan20°+tan20°tan60°+tan60°tan10°=1;
②tan5°tan100°+tan100°tan(-15°)+tan(-15°)tan5°=1;
③tan13°tan35°+tan35°tan42°+tan42°tan13°=1.
一般地,若tanα,tanβ,tanγ都有意义,你从这三个恒等式中猜想得到的一个结论为
当α+β+γ=90°时,tanαtanβ+tanβtanγ+tanγtanα=1
.分析:根据已知中的三角恒等式:①tan10°tan20°+tan20°tan60°+tan60°tan10°=1;②tan5°tan100°+tan100°tan(-15°)+tan(-15°)tan5°=1;③tan13°tan35°+tan35°tan42°+tan42°tan13°=1.我们分析式子中三个角的关系,即可得到答案.
解答:解:分析已知中的三角恒等式:
①tan10°tan20°+tan20°tan60°+tan60°tan10°=1;
②tan5°tan100°+tan100°tan(-15°)+tan(-15°)tan5°=1;
③tan13°tan35°+tan35°tan42°+tan42°tan13°=1.
…
式子左边的三个角和为90°,式子右边均为1,
由此推断当tanα,tanβ,tanγ都有意义时,当α+β+γ=90°时,tanαtanβ+tanβtanγ+tanγtanα=1
故答案为:当α+β+γ=90°时,tanαtanβ+tanβtanγ+tanγtanα=1
①tan10°tan20°+tan20°tan60°+tan60°tan10°=1;
②tan5°tan100°+tan100°tan(-15°)+tan(-15°)tan5°=1;
③tan13°tan35°+tan35°tan42°+tan42°tan13°=1.
…
式子左边的三个角和为90°,式子右边均为1,
由此推断当tanα,tanβ,tanγ都有意义时,当α+β+γ=90°时,tanαtanβ+tanβtanγ+tanγtanα=1
故答案为:当α+β+γ=90°时,tanαtanβ+tanβtanγ+tanγtanα=1
点评:本题考查的知识点是归纳推理,其中根据已知的三角恒等式,分析出式子中三个角的关系,是解答本题的关键.

练习册系列答案
相关题目
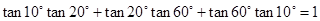 ;
;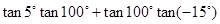
 ;
;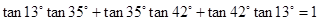 .
. 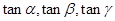 都有意义,你从这三个恒等式中猜想得到的一个结论为 ▲
都有意义,你从这三个恒等式中猜想得到的一个结论为 ▲  ;
;  ;
;
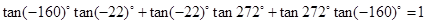
 都有意义,你从这四个恒等式中猜想得到的一个结论为 .
都有意义,你从这四个恒等式中猜想得到的一个结论为 .