题目内容
观察下列几个三角恒等式:
①tan10°tan20°+tan20°tan60°+tan60°tan10°=1;
②tan5°tan100°+tan100°tan(-15°)+tan(-15°)tan5°=1;
③tan13°tan35°+tan35°tan42°+tan42°tan13°=1.
一般地,若tanα,tanβ,tanγ都有意义,你从这三个恒等式中猜想得到的一个结论为
①tan10°tan20°+tan20°tan60°+tan60°tan10°=1;
②tan5°tan100°+tan100°tan(-15°)+tan(-15°)tan5°=1;
③tan13°tan35°+tan35°tan42°+tan42°tan13°=1.
一般地,若tanα,tanβ,tanγ都有意义,你从这三个恒等式中猜想得到的一个结论为
当α+β+γ=90°时,tanαtanβ+tanβtanγ+tanγtanα=1
当α+β+γ=90°时,tanαtanβ+tanβtanγ+tanγtanα=1
.试证明结论.分析:观察所给的4个等式,发现左边都是两个角的正切的乘积形式,一共有三项,且三个角的和为定值:直角,右边的值都为常数1,由此可得结论,再利用和角的正切公式进行证明即可.
解答:解:观察所给的4个等式可得:
若角α,β,γ满足α+β+γ=90°,且tanα,tanβ,tanγ都有意义,则tanαtanβ+tanβtanγ+tanαtanγ=1.
证明如下:∵α+β+γ=90°,∴α+β=90°-γ
∴tan(α+β)=tan(90°-γ)
∴
=
∴tanαtanβ+tanβtanγ+tanγtanα=1
故答案为:当α+β+γ=90°时,tanαtanβ+tanβtanγ+tanγtanα=1
若角α,β,γ满足α+β+γ=90°,且tanα,tanβ,tanγ都有意义,则tanαtanβ+tanβtanγ+tanαtanγ=1.
证明如下:∵α+β+γ=90°,∴α+β=90°-γ
∴tan(α+β)=tan(90°-γ)
∴
| tanα+tanβ |
| 1-tanαtanβ |
| 1 |
| tanγ |
∴tanαtanβ+tanβtanγ+tanγtanα=1
故答案为:当α+β+γ=90°时,tanαtanβ+tanβtanγ+tanγtanα=1
点评:本题考查归纳推理,考查学生分析解决问题的能力,属于基础题.

练习册系列答案
相关题目
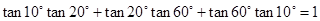 ;
;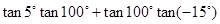
 ;
;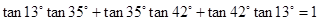 .
. 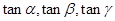 都有意义,你从这三个恒等式中猜想得到的一个结论为 ▲
都有意义,你从这三个恒等式中猜想得到的一个结论为 ▲  ;
;  ;
;
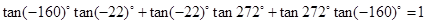
 都有意义,你从这四个恒等式中猜想得到的一个结论为 .
都有意义,你从这四个恒等式中猜想得到的一个结论为 .