题目内容
甲乙两人从4门课程中各选修两门，则甲乙所选的课程中至少有1门不相同的选法共有( )种
| A．30 | B．36 | C．60 | D．72 |
A
解析试题分析：甲、乙所选的课程中至少有1门不相同的选法可以分为两类：
（1）甲、乙所选的课程中2门均不相同，甲先从4门中任选2门，乙选取剩下的2门，有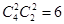
种．
（2）甲、乙所选的课程中有且只有1门相同，分为2步：①从4门中先任选一门作为相同的课程，有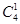
种选法；②甲从剩余的3门中任选1门乙从最后剩余的2门中任选1门有
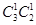种选法，
由分步计数原理此时共有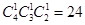
种．
综上，由分类计数原理，甲、所选的课程中至少有1门不相同的选法共有6+24=30种．
考点：计数原理，排列组合.
练习册系列答案
阳光课堂同步练习系列答案
相关题目
圆上有10个点，过每三个点画一个圆内接三角形，则一共可以画的三角形个数为（ ）
| A．720 | B．360 | C．240 | D．120 |
在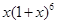
的展开式中，含
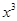项的系数为（ ）
A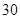． | B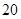． | C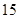． | D． |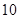
某人将英语单词“apple”记错字母顺序，他可能犯的错误次数最多是(假定错误不重犯)( )
| A．60 | B．59 | C．58 | D．57 |
5名应届毕业生报考三所高校，每人报且仅报一所院校，则不同的报名方法的种数是( )
A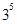． | B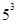． | C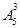． | D． |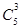
(1＋x)10(1＋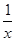
)10展开式中的常数项为( )
| A．1 | B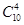．( )2 | C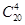． | D． |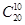
[2013·怀化模拟]将标号为1,2,3,4,5,6的6张卡片放入3个不同的信封中，若每个信封放2张，其中标号为1,2的卡片放入同一信封，则不同的放法共有( )
| A．12种 | B．18种 | C．36种 | D．54种 |
两人进行乒乓球比赛，先赢三局者获胜，决出胜负为止，则所有可能出现的情形（各人输赢局次的不同视为不同情形）共有（ ）
| A．10种 | B．15种 | C．20种 | D．30种 |