题目内容
在 中,
中,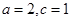 ,则角
,则角 的取值范围是( )
的取值范围是( )
A. | B. | C.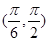 | D. |
D
解析试题分析:因为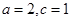 ,所以
,所以 ,从而角
,从而角 ,又由正弦定理可得
,又由正弦定理可得 即
即 ,因为
,因为 ,所以
,所以 ,所以
,所以 ,结合
,结合 可知
可知 ,故选D.
,故选D.
考点:正弦定理.

练习册系列答案
相关题目
 的内角
的内角 所对的边
所对的边 满足
满足 ,且C=60°,则
,且C=60°,则 的值为( )
的值为( )
A. | B. | C.1 | D. |
若满足条件C=60°,AB= ,BC=a的△ABC有两个,那么a的取值范围是 ( )
,BC=a的△ABC有两个,那么a的取值范围是 ( )
A.(1, ) ) | B.( , , ) ) | C.( ,2) ,2) | D.(1,2) |
一艘船上午9:30在A处,测得灯塔S在它的北偏东300处,之后它继续沿正北方向匀速航行,上午10:00到达B处,此时又测得灯塔S在它的北偏东750,且与它相距8 海里,则此船的航速是( )
海里,则此船的航速是( )
| A.24海里/小时 | B.30海里/小时 | C.32海里/小时 | D.40海里/小时 |
在 中,已知
中,已知 ,
, ,则
,则 为( )
为( )
| A.等边三角形 | B.等腰直角三角形 |
| C.锐角非等边三角形 | D.钝角三角形 |
设△ABC的内角A,B,C所对的边分别为a,b,c,若bcosC+ccosB=asinA,则△ABC的形状为( )
| A.直角三角形 | B.锐角三角形 |
| C.钝角三角形 | D.不确定 |
△ABC的内角A,B,C的对边分别为a,b,c,已知b=2,B= ,C=
,C= ,则△ABC的面积为( )
,则△ABC的面积为( )
A.2 +2 +2 | B. +1 +1 |
C.2 -2 -2 | D. -1 -1 |
设△ABC的内角A,B,C所对的边分别为a,b,c,若bcos C+ccos B=asin A,则△ABC的形状为 ( ).
| A.直角三角形 | B.锐角三角形 |
| C.钝角三角形 | D.不确定 |
 ,则该三角形面积的最大值是( )
,则该三角形面积的最大值是( )
