题目内容
(2012•资阳三模)△ABC和△DBC所在的平面相互垂直,且AB=BC=BD,∠CBA=∠DBC=120°,则AD和平面BCD所成的角为( )
分析:作AO⊥BC于点O,连DO,以点O为原点,OD,OC,OA的方向分别为x轴、y轴、z轴方向,建立坐标系,通过求
与平面BCD的夹角去求.
| AD |
解答: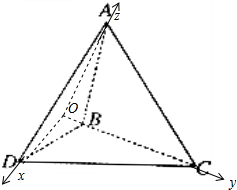 解:设AB=1,作AO⊥BC于点O,连DO,以点O为原点,OD,OC,OA的方向分别为x轴、y轴、z轴方向,建立坐标系,
解:设AB=1,作AO⊥BC于点O,连DO,以点O为原点,OD,OC,OA的方向分别为x轴、y轴、z轴方向,建立坐标系,
得下列坐标:
O(0,0,0)D(
,0,0)B(0,
,0)C(0,
,0)A(0,0,
)
=(
,0,-
),显然
=(0,0,1)为平面BCD的一个法向量
|cos<
,
>|=|
|=|-
|=
∴直线AD与平面BCD所成角的大小90°-45°=45°
故选B.
 解:设AB=1,作AO⊥BC于点O,连DO,以点O为原点,OD,OC,OA的方向分别为x轴、y轴、z轴方向,建立坐标系,
解:设AB=1,作AO⊥BC于点O,连DO,以点O为原点,OD,OC,OA的方向分别为x轴、y轴、z轴方向,建立坐标系,得下列坐标:
O(0,0,0)D(
| ||
| 2 |
| 1 |
| ,2 |
| 3 |
| 2 |
| ||
| ,2 |
| AD |
| ||
| 2 |
| ||
| 2 |
| n1 |
|cos<
| AD |
| n1 |
-
| ||||
|
| ||
| 2 |
| ||
| 2 |
∴直线AD与平面BCD所成角的大小90°-45°=45°
故选B.
点评:本题考查空间角的计算,二面角求解,考查转化的思想方法,计算能力.利用空间向量的知识,降低思维难度,降低空间想象强度,给人们解决问题带来方便.

练习册系列答案
相关题目
 (2012•资阳三模)如图所示,有6个半径都是1的圆,相邻两圆均外切,记集合M={Qi|i=1,2,3,4,5,6}现任取集合M的两个非空子集A,B组成一个有序集合组《A,B》,且满足:集合A中任何一个圆与集合B中任何一个圆均无公共点,则这样的序集合组的个数是( )
(2012•资阳三模)如图所示,有6个半径都是1的圆,相邻两圆均外切,记集合M={Qi|i=1,2,3,4,5,6}现任取集合M的两个非空子集A,B组成一个有序集合组《A,B》,且满足:集合A中任何一个圆与集合B中任何一个圆均无公共点,则这样的序集合组的个数是( )