Question

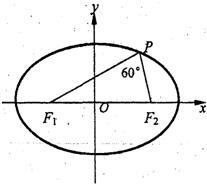已知椭圆C：

x2

a2

+

y2

b2

=1(a＞b＞0)的左、右焦点分别为F₁、F₂，P是椭圆上一点，且∠F₁PF₂=60°，设

|PF1|

|PF2|

=λ
（1）求椭圆C的离心率e和λ的函数关系式e=f（λ）
（2）若椭圆C的离心率e最小，且椭圆C上的动点M到定点N(0，

1

2

)的最远距离为

5

，求椭圆C的方程．

Answer 1

分析：（1）由

|PF1|+|PF2|=2a |PF1|=λ|PF2

?

|PF1|= 2aλ λ+1 |PF2|= 2a λ+1

，由余弦定理，得|F₁F₂|²=|PF₁|²+|PF₂|²-2|PF₁|•|PF₂|cos60°，由此能导出e=f(λ)=

λ2-λ+1

λ+1

(λ＞0)．
（2）由e2=

λ2-λ+1

λ2+2λ+1

=1-

3λ

λ2+2λ+1

=1-

3

λ+ 1 λ +2

，知emin=

1

2

，此时c=

1

2

a，b2=a2-c2=

3

4

a2，则椭圆C的方程为C：

x2

a2

+

4y2

3a2

=1．设M（x，y），又N(0，

1

2

)，则x2=a2-•

4

3

y2|MN|2=x2+(y．-

1

2

)2=(a2-

4

3

y2)+(y2-y+

1

4

)=-

1

3

y2-y+a2+

1

4

=-

1

3

(y+

3

2

)2+a2+1，由此能求出椭圆C的方程．

解答：解：（1）由

|PF1|+|PF2|=2a |PF1|=λ|PF2

?

|PF1|= 2aλ λ+1 |PF2|= 2a λ+1

（2分）
△PF₁F₂，由余弦定理，得|F₁F₂|²=|PF₁|²+|PF₂|²-2|PF₁|•|PF₂|cos60°
即(2c)2=(

2aλ

λ+1

)2+(

2a

λ+1

)2-2•

2aλ

λ+1

•

2a

λ+1

•

1

2

（4分）
上式两边同除以（2a）²，得e2=(

λ

λ+1

)2+(

1

λ+1

)2-

λ

(λ+1)2

=

λ2-λ+1

(λ+1)2

（5分）∴e=f(λ)=

λ2-λ+1

λ+1

(λ＞0)（6分）
（2）由（1）知，e2=

λ2-λ+1

λ2+2λ+1

=1-

3λ

λ2+2λ+1

=1-

3

λ+ 1 λ +2

∵λ＞0，λ+

1

λ

≥2，∴e2≥1-

3

2+2

=

1

4

∴e≥

1

2

，等号当且仅当λ=1时成立，故emin=

1

2

（8分）
此时c=

1

2

a，b2=a2-c2=

3

4

a2，则椭圆C的方程为C：

x2

a2

+

4y2

3a2

=1
设M（x，y），又N(0，

1

2

)，则x2=a2-•

4

3

y2|MN|2=x2+(y．-

1

2

)2=(a2-

4

3

y2)+(y2-y+

1

4

)=-

1

3

y2-y+a2+

1

4

=-

1

3

(y+

3

2

)2+a2+1，
其中y∈[-b，b]．（l0分）
①当-b≤-

3

2

即b≥

3

2

时，则当y=-

3

2

时，|MN

|

2 min

=a2+1=(•

5

)2，得a=2，
则b²=3，b=

3

＞

3

2

，满足条件．（12分）
②当-

3

2

＜-b＜0即0＜b＜

3

2•

时，则当y=-b时，|MN|min=b+

1

2

=

5

，得b=

5

-

1

2

＞

3

2

不满足条件，舍去．综上所述，a=2，b=

3

，所求椭圆C的方程为

x2

4

+

y2

3

=1（14分）

点评：本题考查椭圆的离心率和椭圆方程的求法，解题时要注意余弦定理的合理运用和分类讨论思想的灵活运用．