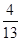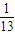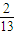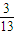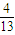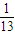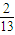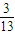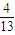题目内容
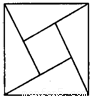
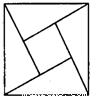
 如图,大正方形的面积是13,四个全等的直角三角形围成一个小正方形.直角三角形的较短边长为2.向大正方形内投一飞镖,则飞镖落在小正方形内的概率为
如图,大正方形的面积是13,四个全等的直角三角形围成一个小正方形.直角三角形的较短边长为2.向大正方形内投一飞镖,则飞镖落在小正方形内的概率为
- A.

- B.
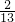
- C.
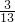
- D.
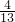
A
分析:根据几何概型概率的求法,飞镖扎在小正方形内的概率为小正方形内与大正方形的面积比,根据题意,可得小正方形的面积与大正方形的面积,进而可得答案.
解答:根据题意,大正方形的面积是13,则大正方形的边长是 ,
,
又直角三角形的较短边长为2,
得出四个全等的直角三角直角边分别是3和2,
则小正方形的边长为1,面积为1;
又∵大正方形的面积为13;
故飞镖扎在小正方形内的概率为 .
.
故选A.
点评:用到的知识点为:概率=相应的面积与总面积之比;难点是得到正方形的边长.
分析:根据几何概型概率的求法,飞镖扎在小正方形内的概率为小正方形内与大正方形的面积比,根据题意,可得小正方形的面积与大正方形的面积,进而可得答案.
解答:根据题意,大正方形的面积是13,则大正方形的边长是
 ,
,又直角三角形的较短边长为2,
得出四个全等的直角三角直角边分别是3和2,
则小正方形的边长为1,面积为1;
又∵大正方形的面积为13;
故飞镖扎在小正方形内的概率为
 .
.故选A.
点评:用到的知识点为:概率=相应的面积与总面积之比;难点是得到正方形的边长.

练习册系列答案
相关题目
 (2013•湖南模拟)如图,大正方形的面积是34,四个全等直角三角形围成一个正方形,直角三角形的较短边长为3,向大正方形内设一飞镖,则飞镖落在小正方形内的概率为( )
(2013•湖南模拟)如图,大正方形的面积是34,四个全等直角三角形围成一个正方形,直角三角形的较短边长为3,向大正方形内设一飞镖,则飞镖落在小正方形内的概率为( )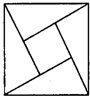 (2012•湖北模拟)如图,大正方形的面积是13,四个全等的直角三角形围成一个小正方形.直角三角形的较短边长为2.向大正方形内投一飞镖,则飞镖落在小正方形内的概率为( )
(2012•湖北模拟)如图,大正方形的面积是13,四个全等的直角三角形围成一个小正方形.直角三角形的较短边长为2.向大正方形内投一飞镖,则飞镖落在小正方形内的概率为( )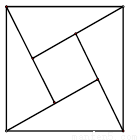
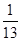 B.
B.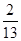 C.
C.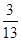 D.
D.