题目内容
(1)解不等式-3<4x-4x2≤0
(2)若不等式mx2+2mx-4<2x2+4x对任意x均成立,求实数m的取值范围
(2)若不等式mx2+2mx-4<2x2+4x对任意x均成立,求实数m的取值范围
(1)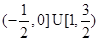 (2)
(2)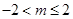
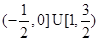 (2)
(2)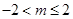
试题分析:(1)根据题意,由于-3<4x-4x2≤0
,那么等价于一个不等式组,可知-3<4x-4x2且4x-4x2≤0,先分析方程的根,结合二次函数图像可知,不等式的解集为
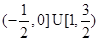
(2)由于不等式mx2+2mx-4<2x2+4x对任意x均成立,那么可知,当m=0,-4<2x2+4x,由于判别式小于零可知成立,恒大于零,当m
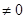 ,要是不等式恒成立,只要开口向上,判别式小于零即可得到
,要是不等式恒成立,只要开口向上,判别式小于零即可得到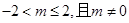 综上可知
综上可知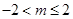
点评:解决的关键是根据一元二次不等式的解法来得到其解集,属于重点试题,要掌握好。

练习册系列答案
相关题目
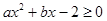 的解集为
的解集为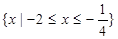 ,则实数
,则实数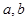 的值为( )
的值为( )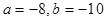


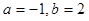
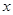 的方程
的方程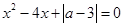 有实根
有实根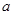 的取值集合
的取值集合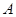
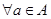 ,不等式
,不等式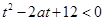 恒成立,求
恒成立,求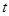 的取值范围
的取值范围 ,对
,对 恒成立,则关于
恒成立,则关于 的不等式
的不等式 的解集为( )
的解集为( ) 



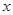 的不等式
的不等式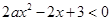 的解集为(2,
的解集为(2,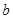 ),则
),则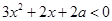 的解集为 .
的解集为 .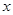 的不等式
的不等式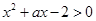 在区间
在区间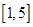 上有解,则实数
上有解,则实数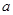 的取值范围为( )
的取值范围为( )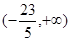

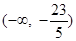
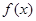 与
与 是定义在同一区间
是定义在同一区间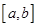 上的两个函数,若对任意的
上的两个函数,若对任意的 ,都有
,都有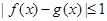 ,则称
,则称 与
与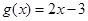 在
在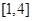
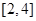
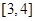
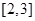
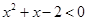 的解集为___________.
的解集为___________.