题目内容
已知函数 ,直线x=m与f(x)和g(x)的图象分别交于M、N两点,则|MN|的最大值 .
,直线x=m与f(x)和g(x)的图象分别交于M、N两点,则|MN|的最大值 .
【答案】分析:先对函数f(x)进行化简,然后表示出函数g(x)的表达式,最后得到|MN|的关系式后根据三角函数的性质可得答案.
解答:解:∵f(x)=sin(x-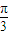 )+
)+ cos(x-
cos(x-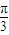 )=2[
)=2[ sin(x-
sin(x-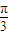 )+
)+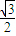 cos(x-
cos(x-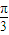 )]
)]
=2sin(x-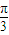 +
+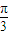 )=2sinx
)=2sinx
∴g(x)=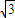 f(
f(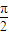 -x)=2
-x)=2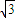 sin(
sin(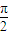 -x)=2
-x)=2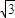 cosx
cosx
又|MN|=|f(m)|+|g(m)|=|2sinm|+|2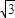 cosm|=4(|
cosm|=4(| sinm|+|
sinm|+|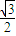 cosm|)=4|sin(m+φ)|
cosm|)=4|sin(m+φ)|
∴|MN|的最大值为4
故答案为:4
点评:本题主要考查两角和与差的应用和正弦函数的图象和性质.属中档题.对于三角函数来说,题目一般不会特别难,但是公式比较多很容易记混,所以要给予重视.
解答:解:∵f(x)=sin(x-
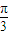 )+
)+ cos(x-
cos(x-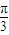 )=2[
)=2[ sin(x-
sin(x-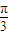 )+
)+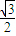 cos(x-
cos(x-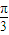 )]
)]=2sin(x-
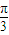 +
+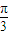 )=2sinx
)=2sinx∴g(x)=
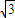 f(
f(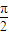 -x)=2
-x)=2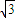 sin(
sin(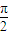 -x)=2
-x)=2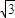 cosx
cosx又|MN|=|f(m)|+|g(m)|=|2sinm|+|2
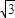 cosm|=4(|
cosm|=4(| sinm|+|
sinm|+|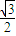 cosm|)=4|sin(m+φ)|
cosm|)=4|sin(m+φ)|∴|MN|的最大值为4
故答案为:4
点评:本题主要考查两角和与差的应用和正弦函数的图象和性质.属中档题.对于三角函数来说,题目一般不会特别难,但是公式比较多很容易记混,所以要给予重视.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
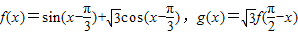 ,直线x=m与f(x)和g(x)的图象分别交于M、N两点,则|MN|的最大值 .
,直线x=m与f(x)和g(x)的图象分别交于M、N两点,则|MN|的最大值 .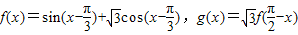 ,直线x=m与f(x)和g(x)的图象分别交于M、N两点,则|MN|的最大值 .
,直线x=m与f(x)和g(x)的图象分别交于M、N两点,则|MN|的最大值 .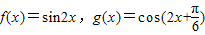 ,直线x=t(t∈R)与函数f(x),g(x)的图象分别交于M,N两点,则|MN|在
,直线x=t(t∈R)与函数f(x),g(x)的图象分别交于M,N两点,则|MN|在 时的最大值为 .
时的最大值为 . ,直线x=m与f(x)和g(x)的图象分别交于M、N两点,则|MN|的最大值 .
,直线x=m与f(x)和g(x)的图象分别交于M、N两点,则|MN|的最大值 .