题目内容
椭圆C的中心在原点,并以双曲线
-
=1的焦点为焦点,以抛物线x2=-6
y的准线到原点的距离为
(1)求椭圆C的方程;
(2)设直线l:y=kx+2(k≠0)与椭圆C相交于A、B两点,使A、B两点关于直线l′:y=mx+1(m≠0)对称,求k的值.
| y2 |
| 4 |
| x2 |
| 2 |
| 6 |
| a2 |
| c |
(1)求椭圆C的方程;
(2)设直线l:y=kx+2(k≠0)与椭圆C相交于A、B两点,使A、B两点关于直线l′:y=mx+1(m≠0)对称,求k的值.
(1)在双曲线
-
=1中,a=2,b=
,c=
=
,
∴焦点为F1(0,-
),F2(,
).
在抛物线x2=-2
y中,p=
,∴准线为y=
.
∴在椭圆中,
=
.从而a=3,b=
.
∴所求椭圆C的方程为
+
=1.
(2)设弦AB的中点为P(x0,y0),则点P是直线l与直线l′的交点,且直线l⊥l′,∴m=-
.
由kAB•
=-
得:k•
=-3,∴ky0=-3x0.…①
由y0=-
•x0+1得:ky0=-x0+k.…②
由①、②得:x0=-
,y0=
.
又∵y0=kx0+2,∴
=-k•
+2,即k2=1,∴k=±1.
在y=kx+2中,当x=0时,y=2,即直线l经过定点M(0,2).
而定点M(0,2)在椭圆的内部,故直线l与椭圆一定相交于两个不同的交点,
∴k的值为±1.
| y2 |
| 4 |
| x2 |
| 2 |
| 2 |
| a2+b2 |
| 6 |
∴焦点为F1(0,-
| 6 |
| 6 |
在抛物线x2=-2
| 6 |
| 6 |
| ||
| 2 |
∴在椭圆中,
| a2 |
| c |
| ||
| 2 |
| 3 |
∴所求椭圆C的方程为
| y2 |
| 9 |
| x2 |
| 3 |
(2)设弦AB的中点为P(x0,y0),则点P是直线l与直线l′的交点,且直线l⊥l′,∴m=-
| 1 |
| k |
由kAB•
| y0 |
| x0 |
| a2 |
| b2 |
| y0 |
| x0 |
由y0=-
| 1 |
| k |
由①、②得:x0=-
| k |
| 2 |
| 3 |
| 2 |
又∵y0=kx0+2,∴
| 3 |
| 2 |
| k |
| 2 |
在y=kx+2中,当x=0时,y=2,即直线l经过定点M(0,2).
而定点M(0,2)在椭圆的内部,故直线l与椭圆一定相交于两个不同的交点,
∴k的值为±1.

练习册系列答案
相关题目

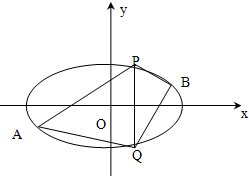 (2013•宜宾一模)已知椭圆C的中心在原点,焦点在x轴上,离心率为
(2013•宜宾一模)已知椭圆C的中心在原点,焦点在x轴上,离心率为