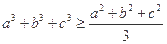题目内容
若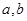 是任意实数,且
是任意实数,且 ,则
,则
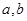 是任意实数,且
是任意实数,且 ,则
,则A. | B. | C. | D. |
B
分析:利用不等式的基本性质可得B,正确,用特值法可排除A、C、D.
解:∵a,b是任意实数,且a>b,
∴不妨令a=0,b=-1,则0<1,可排除A,C,D;
∵y=( )x为单调递减函数,
)x为单调递减函数,
∴a>b时,( )a<(
)a<( )b,
)b,
∴B正确.
故选B.
点评:本题考查不等式的基本性质,着重考查排除法在做选择题的优势,属于基础题.
解:∵a,b是任意实数,且a>b,
∴不妨令a=0,b=-1,则0<1,可排除A,C,D;
∵y=(
 )x为单调递减函数,
)x为单调递减函数,∴a>b时,(
 )a<(
)a<( )b,
)b,∴B正确.
故选B.
点评:本题考查不等式的基本性质,着重考查排除法在做选择题的优势,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
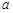 、
、 、
、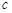 ,下列命题中正确的是( )
,下列命题中正确的是( )

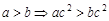
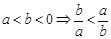
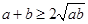

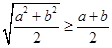
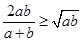
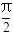 <α<
<α<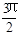 ,
, ,
,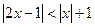
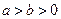 ,求证:
,求证: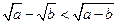 .
.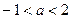 ,
,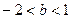 ,则a-b的取值范围是 .
,则a-b的取值范围是 .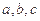 满足
满足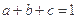 证明
证明