题目内容
已知函数f(x)=lg［(a2－1)x2+(a+1)x+1］
(1)若f(x)的定义域为(－∞,+∞)，求实数a的取值范围；
(2)若f(x)的值域为(－∞,+∞),求实数a的取值范围
(1) a≤－1或a>为
(2) 1≤a≤
解析:
(1）依题意(a2－1）x2+(a+1)x+1>0对一切x∈R恒成立，当a2－1≠0时，其充要条件是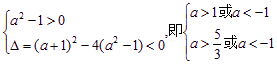
，
∴a＜－1或a>.
又a=－1时，f(x)=0满足题意，a=1时不合题意.
故a≤－1或a>为所求.
(2）依题意只要t=(a2－1)x2+(a+1)x+1能取到(0，+∞）上的任何值，则f(x)的值域为R，故有
,解得1＜a≤,又当a2－1=0即a=1时，t=2x+1符合题意而a=－1时不合题意，∴1≤a≤为所求.
练习册系列答案
相关题目