题目内容
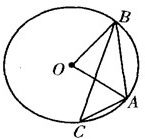选做题：如图，点A，B，C是圆O上的点，且AB=| 2 |
| 3 |
分析：根据所给的一个三角形的两边和一个角，根据正弦定理求出角C，注意这是三角形的一个锐角，根据同弧所对的圆心角等于圆周角的二倍，得到结果．
解答：解：∵在△ABC中，
AB=
，BC=
，∠CAB=120°，
∴根据正弦定理知
=
∴sinC=
，
∵C是三角形的一个锐角，
∴C=45°，
∵∠AOB与∠C对应着圆的同一段弧，
∴∠AOB=90°，
故答案为：90°
AB=
| 2 |
| 3 |
∴根据正弦定理知
| AB |
| sinC |
| BC |
| sin120° |
∴sinC=
| ||
| 2 |
∵C是三角形的一个锐角，
∴C=45°，
∵∠AOB与∠C对应着圆的同一段弧，
∴∠AOB=90°，
故答案为：90°
点评：本题考查正弦定理的应用，考查同弧所对的圆周角等于圆心角的一半，注意做出要用的角的正弦值以后，注意角的范围，本题是一个比较简单的综合题目．
练习册系列答案
相关题目
15、选做题：如图，点A、B、C是圆O上的点，且AB=4，∠ACB=30°，则圆O的面积等于
（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评分）
A：（坐标系与参数方程选做题）在极坐标系中，由θ=0，θ=
（2010•陕西一模）（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评阅记分．）