题目内容
已知abc<0,则在下列四个选项中,表示y=ax2+bx+c的图象只可能是
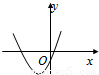
- A.
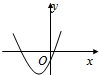
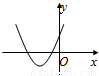
- B.
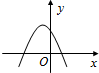
- C.
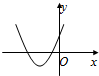
- D.
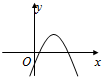
A
分析:根据各选项的图象,确定出a,b,c的正负,验证是否符合abc<0,作出解答.
解答:A 由于图象开口向上,所以a>0.
由图象可知f(0)=c<0,
又抛物线对称轴x= <0,∴b>0,
<0,∴b>0,
符合已知abc<0 所以A正确.
B 由于图象开口向下,所以a<0.
由图象可知f(0)=c>0,
又抛物线对称轴x= <0,∴b<0,
<0,∴b<0,
∴abc>0,与已知abc<0矛盾
所以 B不可能
同样的方法得出C,D均不可能.
故选A.
点评:本题考查二次函数图象,对于二次函数图象要从以下几个方面把握:开口方向,对称轴,与坐标轴交点情况.
分析:根据各选项的图象,确定出a,b,c的正负,验证是否符合abc<0,作出解答.
解答:A 由于图象开口向上,所以a>0.
由图象可知f(0)=c<0,
又抛物线对称轴x=
 <0,∴b>0,
<0,∴b>0,符合已知abc<0 所以A正确.
B 由于图象开口向下,所以a<0.
由图象可知f(0)=c>0,
又抛物线对称轴x=
 <0,∴b<0,
<0,∴b<0,∴abc>0,与已知abc<0矛盾
所以 B不可能
同样的方法得出C,D均不可能.
故选A.
点评:本题考查二次函数图象,对于二次函数图象要从以下几个方面把握:开口方向,对称轴,与坐标轴交点情况.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
已知△ABC中,点D在BC边上,且
=2
,
=r
+s
,则r+s的值是( )
| CD |
| DB |
| CD |
| AB |
| AC |
A、
| ||
B、
| ||
| C、-3 | ||
| D、0 |