题目内容
以下三个命题中:
①设A、B为两个定点,k为非零常数,|PA|-|PB|=k,则动点P的轨迹为双曲线;
②双曲线
-
=1与椭圆
+y2=1有相同的焦点.
③方程2x2-5x+2=0的两根可分别作为椭圆和双曲线的离心率;
其中真命题的序号为
①设A、B为两个定点,k为非零常数,|PA|-|PB|=k,则动点P的轨迹为双曲线;
②双曲线
| x2 |
| 25 |
| y2 |
| 9 |
| x2 |
| 35 |
③方程2x2-5x+2=0的两根可分别作为椭圆和双曲线的离心率;
其中真命题的序号为
②③
②③
(写出所有真命题的序号)分析:(1)根据双曲线的定义知①不正确,(2)求出双曲线的焦点与椭圆的焦点,判定②正确,(3)解方程知两根,一根>0作双曲线的离心率,一根<0作椭圆的离心率,判定③正确;
解答:解:(1)平面内与两个定点F1,F2的距离的差的绝对值等于常数k(k<|F1F2|)的点的轨迹叫做双曲线,
①中当0<k<|AB|时是双曲线的一支,当k=|AB|时,表示射线,∴①不正确;
(2)双曲线
-
=1与椭圆
+y2=1的焦点都是(±
,0),有相同的焦点,∴②正确;
(3)方程2x2-5x+2=0的两根是2和
,2可作为双曲线的离心率,
可作为椭圆的离心率,∴③正确;
故答案为:②③
①中当0<k<|AB|时是双曲线的一支,当k=|AB|时,表示射线,∴①不正确;
(2)双曲线
| x2 |
| 25 |
| y2 |
| 9 |
| x2 |
| 35 |
| 34 |
(3)方程2x2-5x+2=0的两根是2和
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:②③
点评:本题考查了椭圆与双曲线的定义、焦点坐标和离心率等知识,是基础题.

练习册系列答案
相关题目
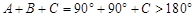 ,这与三角形内角和为
,这与三角形内角和为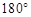 相矛盾,
相矛盾,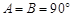 不成立
不成立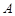 、
、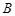 、
、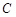 中有两个直角,
中有两个直角,