题目内容
已知正方体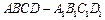 的棱长为2,
的棱长为2,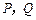 分别是
分别是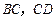 上的动点,且
上的动点,且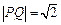 ,确定
,确定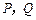 的位置,使
的位置,使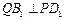 .
.
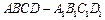 的棱长为2,
的棱长为2,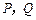 分别是
分别是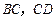 上的动点,且
上的动点,且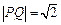 ,确定
,确定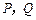 的位置,使
的位置,使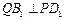 .
.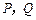 分别为
分别为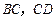 的中点时,
的中点时,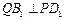

建立如图所示的空间直角坐标系,设 ,
,
得 ,
,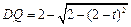 .
.
那么 ,
,
从而 ,
,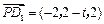 ,
,
由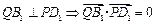 ,
,
即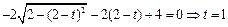 .
.
故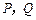 分别为
分别为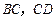 的中点时,
的中点时,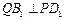 .
.
 ,
,得
 ,
,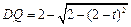 .
.那么
 ,
,从而
 ,
,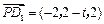 ,
,由
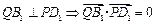 ,
,即
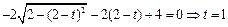 .
.故
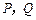 分别为
分别为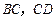 的中点时,
的中点时,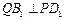 .
.
练习册系列答案
相关题目
题目内容
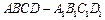 的棱长为2,
的棱长为2,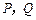 分别是
分别是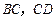 上的动点,且
上的动点,且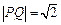 ,确定
,确定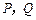 的位置,使
的位置,使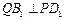 .
.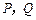 分别为
分别为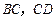 的中点时,
的中点时,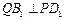

 ,
, ,
,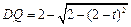 .
. ,
, ,
,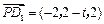 ,
,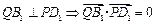 ,
,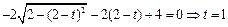 .
.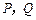 分别为
分别为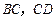 的中点时,
的中点时,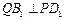 .
.