题目内容
 如图,在四梭锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AD=2,AB=1.点M线段PD的中点.
如图,在四梭锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AD=2,AB=1.点M线段PD的中点.(I)若PA=2,证明:平面ABM⊥平面PCD;
(II)设BM与平面PCD所成的角为θ,当棱锥的高变化时,求sinθ的最大值.
分析:(I)利用线面垂直证明面面垂直即可;
(II)本题难以直接作出直线与平面所成的角,可根据转化思想求出B点到平面的距离,再根据线面角的定义求sinθ关于高的函数,利用函数求最值的方法解决.
(II)本题难以直接作出直线与平面所成的角,可根据转化思想求出B点到平面的距离,再根据线面角的定义求sinθ关于高的函数,利用函数求最值的方法解决.
解答:解:(Ⅰ)证明:∵点M为线段PD的中点,PA=AD=2,∴PD⊥AM.
∵PA⊥平面ABCD,AB?平面ABCD,∴AB⊥PA
又AB⊥AD,∴AB⊥平面PAD,PD?平面PAD
∴PD⊥AB.又AM∩AB=A,
∴PD⊥平面ABM,又PD?平面PCD,
∴平面ABM⊥平面PCD;
(Ⅱ)设点B到平面PCD的距离为d.
∵AB∥CD,∴AB∥平面PCD.
∴点B到平面PCD的距离与点A到平面PCD的距离相等.
过点A在平面PAD内作AN⊥PD于N,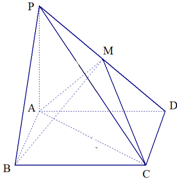
∵平面ABM⊥平面PCD,AN⊥平面PCD.
∴AN就是点A到平面PCD的距离.
设棱锥的高为x,则d=AN=
.
BM=
=
=
=
.
∴sinθ=
=
=
.
∵12+
+x2≥12+2
=12+8
,当且仅当x4=32,即x=2
时,等号成立.
故sinθ≤
=
=2
-2.
∴sinθ的最大值是2
-2.
∵PA⊥平面ABCD,AB?平面ABCD,∴AB⊥PA
又AB⊥AD,∴AB⊥平面PAD,PD?平面PAD
∴PD⊥AB.又AM∩AB=A,
∴PD⊥平面ABM,又PD?平面PCD,
∴平面ABM⊥平面PCD;
(Ⅱ)设点B到平面PCD的距离为d.
∵AB∥CD,∴AB∥平面PCD.
∴点B到平面PCD的距离与点A到平面PCD的距离相等.
过点A在平面PAD内作AN⊥PD于N,

∵平面ABM⊥平面PCD,AN⊥平面PCD.
∴AN就是点A到平面PCD的距离.
设棱锥的高为x,则d=AN=
| 2x | ||
|
BM=
| AB2+AM2 |
AB2+(
|
1+
|
2+
|
∴sinθ=
| d |
| BM |
| 4x | ||
|
| 4 | ||||
|
∵12+
| 32 |
| x2 |
| 32 |
| 2 |
| 4 | 2 |
故sinθ≤
| 4 | ||||
|
| 4 | ||
2+2
|
| 2 |
∴sinθ的最大值是2
| 2 |
点评:本题考查面面垂直的判定、直线与平面所成的角的求法.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
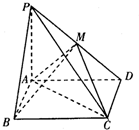 如图,在四梭锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AD=2,AB=1.点M线段PD的中点.
如图,在四梭锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AD=2,AB=1.点M线段PD的中点.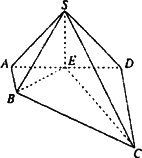
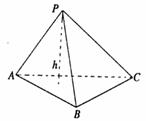
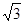 ,SE⊥AD.
,SE⊥AD.