题目内容
20.若直线y=-x+k与曲线x=-$\sqrt{1-{y}^{2}}$恰有一个公共点,则k的取值范围k=-$\sqrt{2}$或k∈(-1,1].分析 把直线和曲线的图象画出来,如图所示,得到曲线为一个半个单位圆,根据直线y=-x+k与曲线x=-$\sqrt{1-{y}^{2}}$恰有一个公共点由图象即可求出k的取值范围.
解答 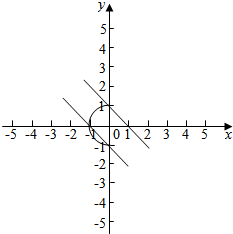 解:根据图象可知:半圆的圆心坐标为(0,0),半径r=1,
解:根据图象可知:半圆的圆心坐标为(0,0),半径r=1,
当直线y=-x+k与y轴的交点的纵坐标在(-1,1]时,直线y=-x+k与曲线x=-$\sqrt{1-{y}^{2}}$恰有一个公共点,即k∈(-1,1];
当直线y=-x+k与半圆在第三象限相切时,直线y=-x+k与曲线x=-$\sqrt{1-{y}^{2}}$恰有一个公共点,
所以圆心到直线的距离d=1,解得k=$\sqrt{2}$(舍去)或k=-$\sqrt{2}$,
综上,k的取值范围是:k=-$\sqrt{2}$或k∈(-1,1].
故答案为:k=-$\sqrt{2}$或k∈(-1,1].
点评 此题考查学生掌握直线与圆相切时满足的关系,灵活运用点到直线的距离公式化简求值,考查了数形结合的数学思想,是一道中档题.根据题意画出函数图象是解本题的关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
12.已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,|F1F2|=2c,点A在椭圆上,且AF1垂直于x轴,$\overrightarrow{A{F}_{1}}$•$\overrightarrow{A{F}_{2}}$=c2,则椭圆的离心率e等于( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}-1}{2}$ | C. | $\frac{\sqrt{5}-1}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |