题目内容

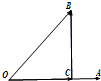精英家教网如图，非零向量
OA
=a，
OB
=b，且
BC
⊥
OA
，C为垂足，设向量
OC
=λa，则λ的值为（　　）
A、
a•b
|a|2
B、
a•b
|a|•|b|
C、
a•b
|b|2
D、
|a|•|b|
a•b
分析：利用向量垂直数量积为零找出λ满足的方程解之
解答：解：
CB
=
OC
-
OB
，
BC
⊥
OA
，
OC
=λa
∴
OC
⊥
CB
，
∴
OC
•
CB
 =0
即
OC
•
CB
=
OC•
( 
OC
-
OB
)=λ
a
•(λ
a
-
b
)=λ2
a
2-λ
a
•
b
=0
∴λ=
a•b
|a|2

故选项为A
点评：向量垂直的充要条件．
练习册系列答案
相关题目
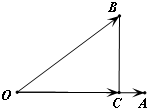如图，非零向量
OA
=
a
，
OB
=
b
，且BC⊥OA，C为垂足，若
OC
=λ
a
，则λ=（　　）
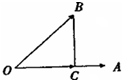如图，非零向量
OA
=
a
，
OB
=
b
，且BC⊥OA，C为垂足，若
OC
=λ
a
，则λ=（　　）
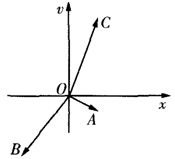精英家教网如图，非零向量
OA
，
OB
与x轴正半轴的夹角分别为
π
6
和
2π
3
，且
OA
+
OB
+
OC
=0，则
OC
与x轴正半轴的夹角的取值范围是
 
．
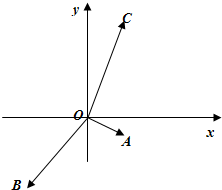如图，非零向量
OA
，
OB
与x轴正半轴的夹角分别为 
π
6
和
2π
3
，且
OA
+
OB
+
OC
=
0
，则
OC
与x轴正半轴的夹角的取值范围是．（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网