题目内容
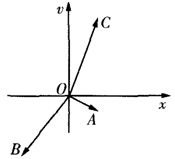如图，非零向量| OA |
| OB |
| π |
| 6 |
| 2π |
| 3 |
| OA |
| OB |
| OC |
| OC |
分析：根据两个向量与横轴的正方向所成的角，和这两个向量没有给出模长，估计两个向量的和与横轴正方向的夹角，根据
与这两个向量的和在同一条直线上，得到范围．
| OC |
解答：解：∵
+
+
=0，
∴
=-(
+
)
∵条件中没有给出两个向量的模长，
∵非零向量
，
与x轴正半轴的夹角分别为
和
，
∴这两个向量的和与x轴正半轴的夹角的取值是（
，
）
∴
与x轴正半轴的夹角的取值范围是（
，
）
故答案为：（
，
）
| OA |
| OB |
| OC |
∴
| OC |
| OA |
| OB |
∵条件中没有给出两个向量的模长，
∵非零向量
| OA |
| OB |
| π |
| 6 |
| 2π |
| 3 |
∴这两个向量的和与x轴正半轴的夹角的取值是（
| π |
| 6 |
| 2π |
| 3 |
∴
| OC |
| π |
| 3 |
| 5π |
| ，6 |
故答案为：（
| π |
| 3 |
| 5π |
| ，6 |
点评：本题考查两个向量的和的问题，在解题时注意两个向量的模长是一个未知量，这样就可以估计出两个向量的夹角的范围，注意在图形中认真观察．
练习册系列答案
相关题目
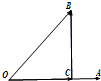如图，非零向量| OA |
| OB |
| BC |
| OA |
| OC |
A、
| ||
B、
| ||
C、
| ||
D、
|
如图，非零向量
如图，非零向量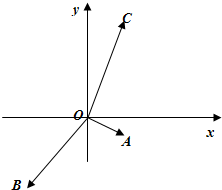
如图，非零向量