题目内容
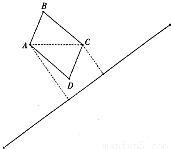
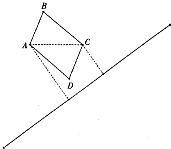 如图,在一段笔直的国道同侧有相距120米的A,C两处,点A,C到国道的距离分别是119米、47米,拟规划建设一个以AC为对角线的平行四边形ABCD的临时仓库,且四周围墙总长为400米,根据公路法以及省公路管理条例规定:建筑物离公路距离不得少于20米.若将临时仓库面积建到最大,该规划是否符合规定?
如图,在一段笔直的国道同侧有相距120米的A,C两处,点A,C到国道的距离分别是119米、47米,拟规划建设一个以AC为对角线的平行四边形ABCD的临时仓库,且四周围墙总长为400米,根据公路法以及省公路管理条例规定:建筑物离公路距离不得少于20米.若将临时仓库面积建到最大,该规划是否符合规定?
解:由题意,|AB|+|CB|=|DA|+|DC|=200>160,所以平行四边形基地的另两个顶点B,D在以A,C为焦点的椭圆上
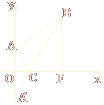
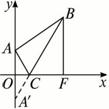
以AC所在直线为x轴,AC中点为原点建立直角坐标系,可得椭圆方程为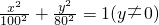
设公路所在直线l与x轴相交于点E,且CE=x米,则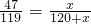 ,∴x=
,∴x= ,即点E(
,即点E(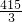 ,0)
,0)
∴直线l的方程为:3x-4y-415=0
当C,D分别为椭圆短轴的两个端点时,临时仓库占地面积最大,此时D(0,-80),
点D到直线l的距离为 =19<20
=19<20
∴该规划不符合规定.
分析:由题意,|AB|+|CB|=|DA|+|DC|=200>160,所以平行四边形基地的另两个顶点B,D在以A,C为焦点的椭圆上,建立坐标系求出椭圆的方程,求出公路所在直线l的方程,当C,D分别为椭圆短轴的两个端点时,临时仓库占地面积最大,求出点D到直线l的距离,即可得到结论.
点评:本题考查椭圆的应用,考查椭圆的定义与标准方程,考查点到直线距离公式,属于中档题.
以AC所在直线为x轴,AC中点为原点建立直角坐标系,可得椭圆方程为
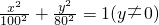
设公路所在直线l与x轴相交于点E,且CE=x米,则
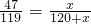 ,∴x=
,∴x= ,即点E(
,即点E(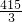 ,0)
,0)∴直线l的方程为:3x-4y-415=0
当C,D分别为椭圆短轴的两个端点时,临时仓库占地面积最大,此时D(0,-80),
点D到直线l的距离为
 =19<20
=19<20∴该规划不符合规定.
分析:由题意,|AB|+|CB|=|DA|+|DC|=200>160,所以平行四边形基地的另两个顶点B,D在以A,C为焦点的椭圆上,建立坐标系求出椭圆的方程,求出公路所在直线l的方程,当C,D分别为椭圆短轴的两个端点时,临时仓库占地面积最大,求出点D到直线l的距离,即可得到结论.
点评:本题考查椭圆的应用,考查椭圆的定义与标准方程,考查点到直线距离公式,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
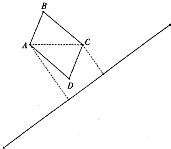 (2012•厦门模拟)如图,在一段笔直的国道同侧有相距120米的A,C两处,点A,C到国道的距离分别是119米、47米,拟规划建设一个以AC为对角线的平行四边形ABCD的临时仓库,且四周围墙总长为400米,根据公路法以及省公路管理条例规定:建筑物离公路距离不得少于20米.若将临时仓库面积建到最大,该规划是否符合规定?
(2012•厦门模拟)如图,在一段笔直的国道同侧有相距120米的A,C两处,点A,C到国道的距离分别是119米、47米,拟规划建设一个以AC为对角线的平行四边形ABCD的临时仓库,且四周围墙总长为400米,根据公路法以及省公路管理条例规定:建筑物离公路距离不得少于20米.若将临时仓库面积建到最大,该规划是否符合规定?