题目内容
已知椭圆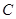 方程为
方程为 ,过右焦点斜率为1的直线到原点的距离为
,过右焦点斜率为1的直线到原点的距离为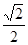 .
.
(1)求椭圆方程.
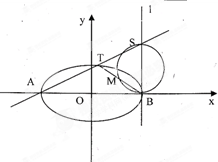
(2)已知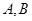 为椭圆的左右两个顶点,
为椭圆的左右两个顶点,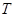 为椭圆在第一象限内的一点,
为椭圆在第一象限内的一点,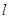 为过点
为过点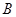 且垂直
且垂直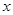 轴的直线,点
轴的直线,点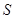 为直线
为直线 与直线
与直线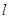 的交点,点
的交点,点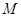 为以
为以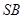 为直径的圆与直线
为直径的圆与直线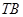 的一个交点,求证:
的一个交点,求证: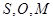 三点共线.
三点共线.
(1) ;(2)详见解析.
;(2)详见解析.
解析试题分析:(1)由过右焦点斜率为1的直线到原点的距离为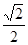 可以得到右焦点坐标,即
可以得到右焦点坐标,即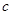 的值.再由公式
的值.再由公式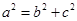 可得椭圆方程.此处注意因为是右焦点,即焦点在
可得椭圆方程.此处注意因为是右焦点,即焦点在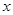 轴上,从而得到
轴上,从而得到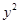 对应的分母1即为
对应的分母1即为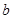 ;(2)由
;(2)由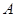 点坐标设出直线
点坐标设出直线 的点斜式方程,联立椭圆方程求出
的点斜式方程,联立椭圆方程求出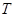 的坐标.易知直线
的坐标.易知直线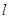 的方程,所以易求得
的方程,所以易求得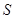 点坐标,由圆的性质知
点坐标,由圆的性质知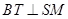 ,则只要
,则只要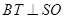 就有直线
就有直线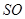 、
、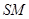 重合,即
重合,即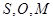 三点共线.因为点的坐标已求得,
三点共线.因为点的坐标已求得,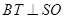 可通过向量数量积予以证明.注意本题如选择求
可通过向量数量积予以证明.注意本题如选择求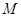 点坐标则将较为繁琐,增加了解题的计算量,这里合理利用圆的直径对应的圆周角是直角这一性质,简化了运算.
点坐标则将较为繁琐,增加了解题的计算量,这里合理利用圆的直径对应的圆周角是直角这一性质,简化了运算.
试题解析:(1)设右焦点为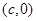 ,则过右焦点斜率为1的直线方程为:
,则过右焦点斜率为1的直线方程为: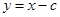 1分
1分
则原点到直线的距离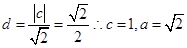 3分
3分 方程
方程 4分
4分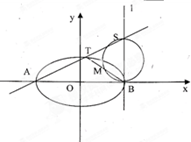
(2)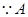 点坐标为
点坐标为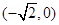 5分
5分
设直线 方程为:
方程为: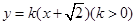 ,设点
,设点 坐标为
坐标为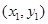
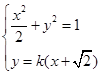 得:
得: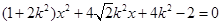 6分
6分 7分
7分
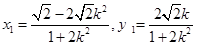 9分
9分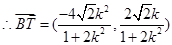 10分
10分
由圆的性质得: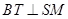
又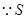 点的横坐标为
点的横坐标为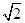
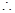
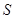 点的坐标为
点的坐标为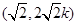 11分
11分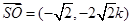 11分
11分 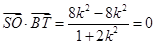 13分
13分
即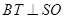 ,又
,又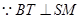
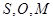 三点共线 14分
三点共线 14分
考点:1.直线与圆锥曲线的位置关系;2.直线的方程;3.平面向量的应用.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
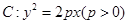 的焦点为
的焦点为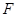 ,准线为
,准线为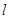 ,
,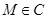 ,以
,以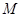 为圆心的圆
为圆心的圆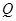 ,
,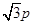 ,
,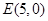 是圆
是圆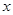 轴除
轴除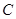 与圆
与圆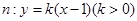 ,
,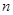 与
与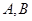 两点,
两点,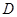 ,且
,且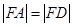 , 求
, 求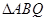 的面积.
的面积. :
: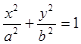
 ,
,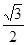 ,求椭圆的标准方程;
,求椭圆的标准方程; 的直线
的直线 与椭圆
与椭圆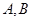 ,且
,且 为锐角(
为锐角( 为坐标原点),求直线
为坐标原点),求直线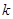 的取值范围;
的取值范围;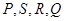 四点,设原点
四点,设原点 的一边距离为
的一边距离为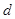 ,试求
,试求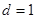 时
时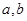 满足的条件.
满足的条件.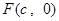 是椭圆
是椭圆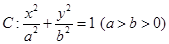 的右焦点,圆
的右焦点,圆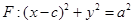 与
与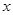 轴交于
轴交于 两点,
两点, 是椭圆
是椭圆 与圆
与圆 的一个交点,且
的一个交点,且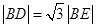
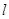 与
与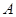 ,且
,且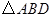 的面积为
的面积为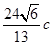 ,求椭圆
,求椭圆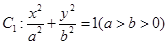 的离心率为
的离心率为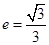 ,直线
,直线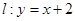 与以原点为圆心、以椭圆
与以原点为圆心、以椭圆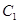 的短半轴长为半径的圆
的短半轴长为半径的圆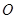 相切.
相切.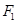 ,右焦点为
,右焦点为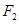 ,直线
,直线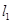 过点
过点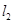 垂直于
垂直于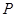 ,线段
,线段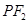 的垂直平分线交
的垂直平分线交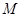 ,求点
,求点 的方程;
的方程;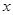 轴交于点
轴交于点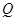 ,不同的两点
,不同的两点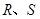 在
在 ,求
,求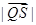 的取值范围.
的取值范围.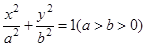 的离心率为
的离心率为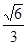 ,且过点
,且过点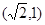 .
.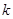 的直线
的直线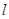 与椭圆相交于不同的两点
与椭圆相交于不同的两点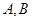 ,试问在
,试问在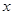 轴上是否存在点
轴上是否存在点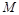 ,使
,使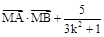 是与
是与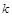 无关的常数?若存在,求出点
无关的常数?若存在,求出点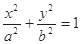 (
(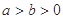 )右顶点到右焦点的距离为
)右顶点到右焦点的距离为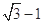 ,短轴长为
,短轴长为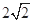 .
.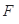 的直线与椭圆分别交于
的直线与椭圆分别交于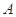 、
、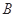 两点,若线段
两点,若线段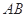 的长为
的长为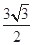 ,求直线
,求直线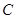 的中心在坐标原点,右准线为
的中心在坐标原点,右准线为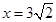 ,离心率为
,离心率为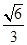 .若直线
.若直线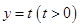 与椭圆
与椭圆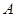 、
、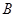 ,以线段
,以线段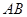 为直径作圆
为直径作圆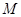 .
.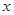 轴相切,求圆
轴相切,求圆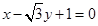 截得的线段长.
截得的线段长.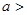
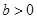 ,曲线
,曲线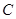 上任意一点
上任意一点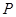 分别与点
分别与点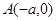 、
、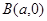 连线的斜率的乘积为
连线的斜率的乘积为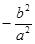 .
.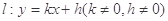 与
与 轴、
轴、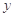 轴分别交于
轴分别交于 、
、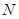 两点,若曲线
两点,若曲线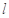 没有公共点,求证:
没有公共点,求证: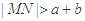 .
.