题目内容
f（x）=x2+2ax+1在[1，2]上是单调函数，则a的取值范围是________．
a≤-2或a≥-1
分析：根据二次函数在闭区间[-1，2]上为单调函数，得到抛物线的对称轴小于等于1或大于等于2，即可求出a的取值范围．
解答：∵f（x）=x2+2ax+1在[1，2]上是单调函数，
∴x=-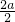
=-a≤1或-a≥2，
解得：a≤-2或a≥-1．
故答案为：a≤-2或a≥-1．
点评：此题考查了二次函数的性质，由函数在闭区间上单调找出对称轴的范围是解本题的关键．
分析：根据二次函数在闭区间[-1，2]上为单调函数，得到抛物线的对称轴小于等于1或大于等于2，即可求出a的取值范围．
解答：∵f（x）=x2+2ax+1在[1，2]上是单调函数，
∴x=-
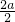=-a≤1或-a≥2，解得：a≤-2或a≥-1．
故答案为：a≤-2或a≥-1．
点评：此题考查了二次函数的性质，由函数在闭区间上单调找出对称轴的范围是解本题的关键．
练习册系列答案
相关题目