题目内容
已知实数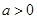 ,函数
,函数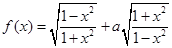 .
.
(1)当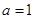 时,求
时,求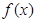 的最小值;
的最小值;
(2)当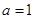 时,判断
时,判断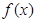 的单调性,并说明理由;
的单调性,并说明理由;
(3)求实数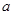 的范围,使得对于区间
的范围,使得对于区间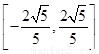 上的任意三个实数
上的任意三个实数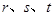 ,都存在以
,都存在以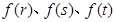 为边长的三角形.
为边长的三角形.
(1)2;(2)递增;(3)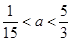 .
.
【解析】
试题分析:(1)研究函数问题,一般先研究函数的性质,如奇偶性,单调性,周期性等等,如本题中函数 是偶函数,因此其最小值我们只要在
是偶函数,因此其最小值我们只要在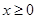 时求得即可;(2)
时求得即可;(2)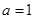 时,
时, 可化简为
可化简为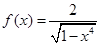 ,下面我们只要按照单调性的定义就可证明在
,下面我们只要按照单调性的定义就可证明在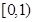 上函数是单调递增的,当然在
上函数是单调递增的,当然在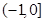 上是递减的;(3)处理此问题,首先通过换元法把问题简化,设
上是递减的;(3)处理此问题,首先通过换元法把问题简化,设 ,则函数
,则函数 变为
变为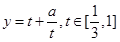 ,问题变为求实数
,问题变为求实数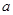 的范围,使得在区间
的范围,使得在区间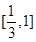 上,恒有
上,恒有 .对于函数
.对于函数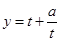 ,我们知道,它在
,我们知道,它在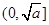 上递减,在
上递减,在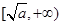 上递增,故我们要讨论它在区间
上递增,故我们要讨论它在区间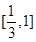 上的最大(小)值,就必须分类讨论,分类标准显然是
上的最大(小)值,就必须分类讨论,分类标准显然是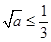 ,
,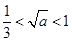 ,
,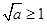 ,在
,在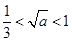 时还要讨论最大值在区间
时还要讨论最大值在区间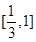 的哪个端点取得,也即共分成四类.
的哪个端点取得,也即共分成四类.
试题解析:易知 的定义域为
的定义域为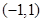 ,且
,且 为偶函数.
为偶函数.
(1)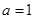 时,
时,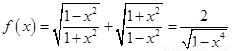 2分
2分
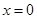 时
时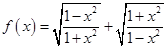 最小值为2.
4分
最小值为2.
4分
(2) 时,
时,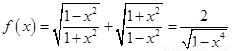
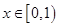 时,
时,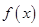 递增;
递增;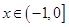 时,
时,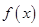 递减;
6分
递减;
6分
 为偶函数.所以只对
为偶函数.所以只对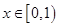 时,说明
时,说明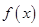 递增.
递增.
设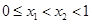 ,所以
,所以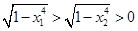 ,得
,得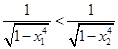
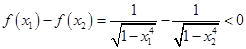
所以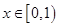 时,
时,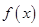 递增;
10分
递增;
10分
(3) ,
,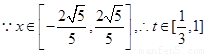 ,
,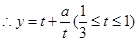
从而原问题等价于求实数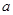 的范围,使得在区间
的范围,使得在区间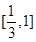 上,
上,
恒有 . 11分
. 11分
①当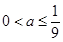 时,
时,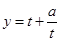 在
在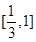 上单调递增,
上单调递增,
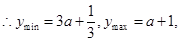 由
由 得
得 ,
,
从而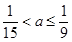 ;
12分
;
12分
②当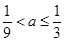 时,
时,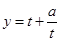 在
在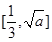 上单调递减,在
上单调递减,在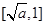 上单调递增,
上单调递增,
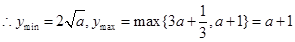 ,
,
由 得
得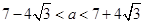 ,从而
,从而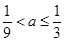 ; 13分
; 13分
③当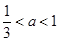 时,
时,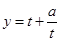 在
在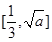 上单调递减,在
上单调递减,在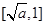 上单调递增,
上单调递增,
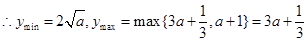 ,
,
由 得
得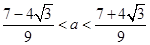 ,从而
,从而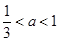 ; 14分
; 14分
④当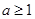 时,
时,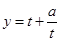 在
在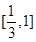 上单调递减,
上单调递减,
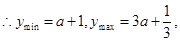
由 得
得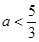 ,从而
,从而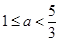 ;
15分
;
15分
综上,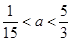 .
16分
.
16分
考点:(1)函数的最值;(2)函数的单调性的证明;(3)分类讨论与函数的最值.

 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案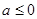 ,函数
,函数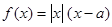 .
.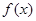 在
在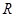 上的奇偶性;
上的奇偶性;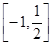 上的最大值。
上的最大值。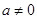 ,函数
,函数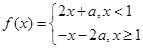 ,若
,若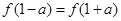 ,则
,则 的值为 .
的值为 .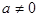 ,函数
,函数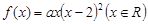 .
.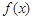 有极大值32,求实数
有极大值32,求实数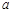 的值;
的值;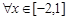 ,不等式
,不等式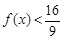 恒成立,求实数
恒成立,求实数 ,函数
,函数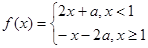 ,若
,若 ,则a的
,则a的