题目内容
(本题满分14分,第1小题8分,第2小题6分)
(理) 的周长为
的周长为 。
。
(1)求函数 的解析式 ,并写出函数的定义域;
的解析式 ,并写出函数的定义域;
(2)求函数 的值域。
的值域。
(文)设函数
(1)求函数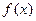 的最大值和及相应的
的最大值和及相应的 的值;
的值;
(2)设A,B,C为 的三个内角,
的三个内角, ,求角C的大小及
,求角C的大小及 边的长。
边的长。
(理)
 的周长为
的周长为 。
。(1)求函数
 的解析式 ,并写出函数的定义域;
的解析式 ,并写出函数的定义域;(2)求函数
 的值域。
的值域。(文)设函数

(1)求函数
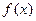 的最大值和及相应的
的最大值和及相应的 的值;
的值;(2)设A,B,C为
 的三个内角,
的三个内角, ,求角C的大小及
,求角C的大小及 边的长。
边的长。(理)(1)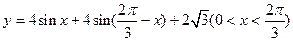
(2)函数的值域是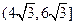
(文)(1)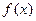 的最大值为1, 此时
的最大值为1, 此时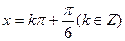
(2)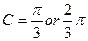 ,
,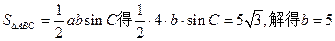
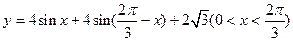
(2)函数的值域是
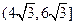
(文)(1)
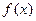 的最大值为1, 此时
的最大值为1, 此时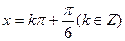
(2)
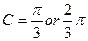 ,
,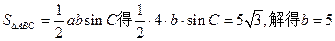
解:(理)(1) 的内角和A+B+C=
的内角和A+B+C=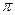 ,
,
且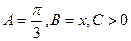

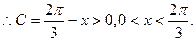
由正弦定理,知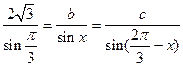 ,
,
即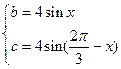 ……………………4分
……………………4分
所以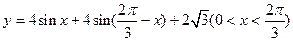 …………
………… …………4分
…………4分
(2)由(1)知,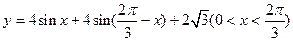
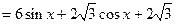
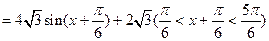 ………………3分
………………3分
由正弦函数的图像知,当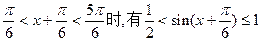
于是,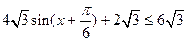 ,
,
所以,函数的值域是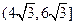 ………………3分
………………3分
(文)(1)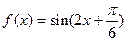 ………………4分
………………4分
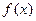 的最大值为1 ………………2分
的最大值为1 ………………2分
此时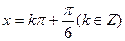 ………………2分
………………2分
(2)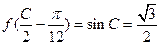 ………………2分
………………2分
从而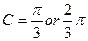
由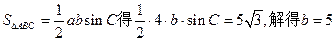 ………………2分
………………2分
 的内角和A+B+C=
的内角和A+B+C=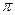 ,
,且
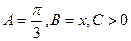

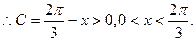
由正弦定理,知
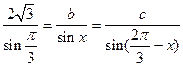 ,
,即
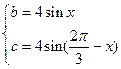 ……………………4分
……………………4分所以
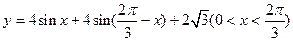 …………
………… …………4分
…………4分(2)由(1)知,
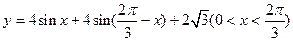
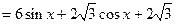
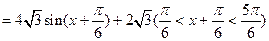 ………………3分
………………3分由正弦函数的图像知,当
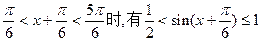
于是,
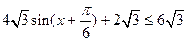 ,
,所以,函数的值域是
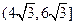 ………………3分
………………3分(文)(1)
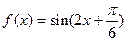 ………………4分
………………4分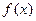 的最大值为1 ………………2分
的最大值为1 ………………2分此时
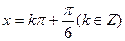 ………………2分
………………2分(2)
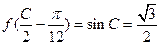 ………………2分
………………2分从而
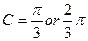
由
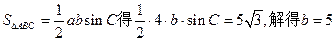 ………………2分
………………2分
练习册系列答案
相关题目

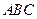 中,角
中,角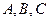 所对的边分别为
所对的边分别为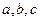 ,已知
,已知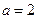 ,
,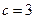 ,
,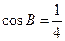 .
.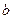 的值;
的值; 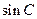 的值.
的值. 中,已知
中,已知 ,
, ,▲▲,求角
,▲▲,求角 的大小.”经推断缺少的条件为三角形一边的长度,且答案提示
的大小.”经推断缺少的条件为三角形一边的长度,且答案提示 ,试将所缺的条件补充完整.
,试将所缺的条件补充完整.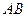 ,可以选与塔底在同一水平面内
,可以选与塔底在同一水平面内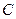 与
与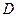 .如图所示,测得
.如图所示,测得 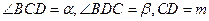
 ,则
,则 米。
米。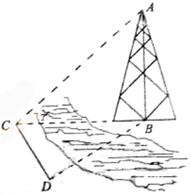
 中,角
中,角 所对的边分别是
所对的边分别是 ,若
,若 ,且
,且 ,则
,则 中,
中,  分别是
分别是 的对边,若
的对边,若 ,则
,则 时,可以选与塔底
时,可以选与塔底 在同一水平面内的两个测点
在同一水平面内的两个测点 与
与 .测得
.测得  米,并在点
米,并在点 的仰角为
的仰角为 ,则塔高AB= 米;
,则塔高AB= 米;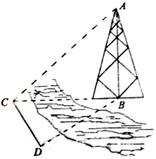
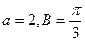 ,若△ABC的面积为
,若△ABC的面积为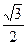 ,则tanC为( )
,则tanC为( )
