题目内容
某工厂生产某种产品固定成本为2000万元,并且每生产一单位产品,成本增加10万元,又知总收入k是单位产品数Q的函数,k(Q)=40Q-
Q2,则总利润L(Q)的最大值是
| 1 | 20 |
2500万元
2500万元
.分析:先计算单位产品数Q时的总成本,再确定利润L(Q),利用配方法,即可求得结论.
解答:解:∵每生产一单位产品,成本增加10万元,∴单位产品数Q时的总成本为2000+10Q万元
∵k(Q)=40Q-
Q2,
∴利润L(Q)=40Q-
Q2-10Q-2000=-
Q2+30Q-2000=-
(Q-300)2+2500
∴Q=300时,利润L(Q)的最大值是2500万元
故答案为:2500万元
∵k(Q)=40Q-
| 1 |
| 20 |
∴利润L(Q)=40Q-
| 1 |
| 20 |
| 1 |
| 20 |
| 1 |
| 20 |
∴Q=300时,利润L(Q)的最大值是2500万元
故答案为:2500万元
点评:本题考查利用数学知识解决实际问题,考查配方法的运用,正确确定函数表达式是关键.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
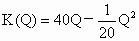 ,则总利润L(Q)的最大值是_____.
,则总利润L(Q)的最大值是_____. Q2,则总利润L(Q)的最大值是________.
Q2,则总利润L(Q)的最大值是________.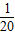 Q2,则总利润L(Q)的最大值是 .
Q2,则总利润L(Q)的最大值是 .