题目内容
函数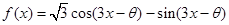
是奇函数，则
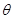等于
A． | B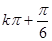． | C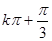． | D． |
D
解析试题分析：根据题意，由于函数
，由于为奇函数，那么可知
，那么可知答案为，选D.
考点：三角函数的奇偶性
点评：解决的关键是对于三角函数关系式的化简变形为单一三角函数，然后借助于三角函数的性质来得到，属于基础题。
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
设
，则
是 ( )
A．周期为 的奇函数 | B．周期为的偶函数 | C．周期为 的奇函数 | D．周期为的偶函数 |
已知函数
，若
，则
与
的大小关系是（ ）
| A．> | B．< |
| C．= | D．大小与a、 有关 |
最小值是 ( )
| A．-1 | B． | C． | D．1 |
若动直线
与函数
和
的图像分别交于
两点，则
的最大值为（ ）
| A．1 | B． | C． | D．2 |
的部分图象大致是（ ）
已知函数y=2sin（2x+
）（||<
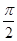）的图象经过点（0，1），则该函数的一条对称轴方程为
A．x= | B．x= | C．x=－ | D．x=－ |
，则
的值为（ ）
A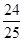． | B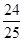．－ | C． | D． |
角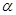
的顶点在坐标原点，始边在X轴非负半轴，
为角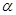终边上一点，则
( )
A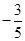． | B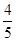． | C． | D． |